Dämpfungsfaktor nochmal erklärt (aus wenn's überheblich klingt - ist es aber nicht)

Nun tragen wir die gefundenen Ergebnisse in einem Koordinatensystem auf, prozentuale Abweichungen als Funktion des Signalzeitpunktes:



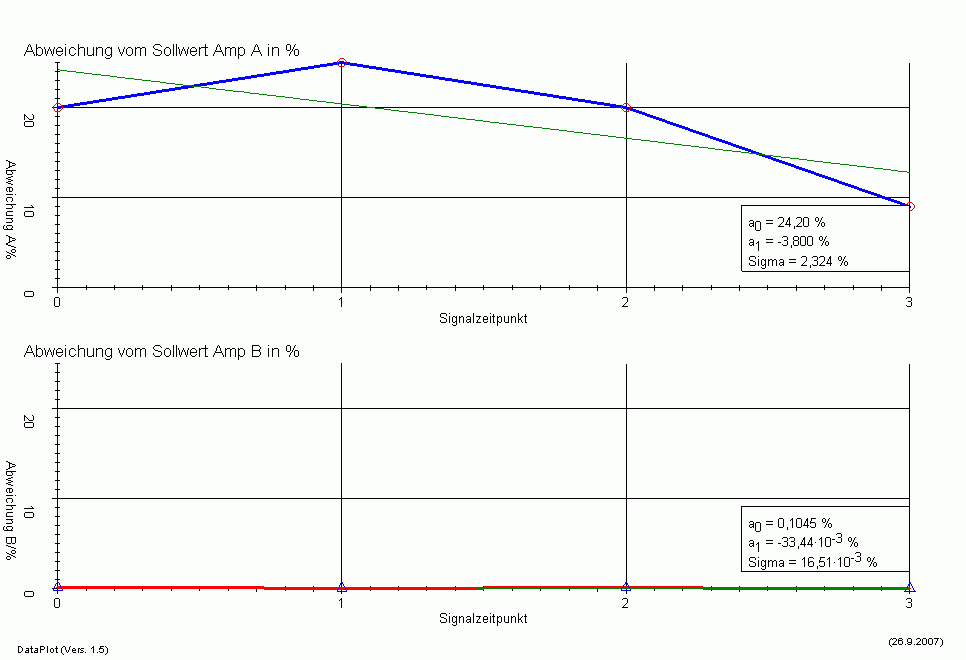
Ich gehe mal davon aus, diese beiden bewußt gleich skalierten Diagramme kapiert nun jeder? Deutlicher ist es kaum noch darzustellen, der "böse" Verstärker mit dem sehr niedrigen dynamischen Innnenwiderstand (sehr hoher Dämpfungsfaktor) kommt wesentlich besser mit der schwankenden Lastimpedanz zurecht als der Verstärker, bei dem es angeblich immer egal sein soll, dass der Dämpfungsfaktor niedrig ist.

Beim blauen Verstärker A würde an dieser schwierigen Last alleine schon der niedrige Dämfungsfaktor einen erhöhten Klirrfaktor bewirken, der rote Verstärker B mit hohem Dämpfungsfaktor steckt das ganz locker weg und verzerrt kaum. Diesen blauen Verstärker A könnte man nur noch einigermaßen sinnvoll betreiben an einem Lautsprecher, der eine kostante Impedanz aufweist, wieder besser gesagt eine konstante Summe aus Kabel+Weiche+Lautsprecher.

Also hoffentlich hat es jeder jetzt endlich verstanden?

Der Satz der Konstantheit: was zählt ist ein konstanter Dämpfungsfaktor, konstant über Frequenz und auch konstant über Amplitude und auch konstant über gezogenem Strom - nichts anderes - dieser Satz der Konstantheit ist umso wichtiger je niedriger der angesetzte normierte Dämpfungsfaktor ist, bei einem Verstärker mit DF 40 gewinnt der Satz der Konstantheit an Bedeutung wenn das Teil z.B. zwischen 35 und 45 schwankt. Bei einem Verstärker mit einem angesetzten normierten Dämpfungsfaktor von 40000, da ist es dann relativ wurscht wenn der DF mal zwischen 20000 und 60000 schwanken würde. Das ist dann genau deswegen weniger wichtig, da die resultierende fehlende Sollspannung am Ausgang sich dann kaum verändern würde, ob nun 0.003% oder 0.001% fehlen hört doch kein Fatzke mehr? Nur der Unterschied zwischen 1% und 5% fehlende Sollspannung das merkt auch ein Fatzke.

Nur einfach zu sagen, hohe Dämpfungsfaktoren braucht man nicht ist purer Schwachsinn - das ist unfair dem Verstärker gegenüber. Ein hoher Dämpfungsfaktor unter allen Frequenzen, Amplitunden und Stromentnahme ist etwas schönes, nützliches und gibt Sicherheit bei schwierigen Lasten, ist aber niemals etwas schädliches - wer das Gegenteil behauptet hat keine Ahnung von der Materie.

Nochmal, einen niedrigen Dämpfungsfaktor anzustreben macht überhaupt keinen elektrotechnischen Sinn; man muss es aber jetzt so sagen und diesen einen einzigen Sonderfall nennen, ein niedriger Dämpfungsfaktor wird genau dann egal wenn genau diese beiden Bedingungen erfüllt sind:

Dämpfungsfaktor niedrig, aber konstant über Frequenz, Amplitude und Stromentnahme

bei gleichzeitig!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

konstanter Impedanz der Reihenschaltung aus Kabel+Weiche+Lautsprecher, konstant über Frequenz, Amplitude und Stromaufnahme (diesen LS muss man halt erst bauen, das ist das Problem). 

Die prozentuale Abnahme vom Sollwert wäre dann ein konstanter Wert, was wiederum keinen zusätzlichen Klirrfaktor durch den Dämpfungsfaktor bedeuten würde. Das ist genau der Grund warum an Verstärkern mit schlechten Dämpfungsfaktoren der Einfluß der verschiedenen Lautsprecher sehr bedeutend wird und der Verstärker an einem LS wenig Klirr produziert und an einem anderen LS brutal klirren kann. Im Gegenzug erklärt das auch, bei einem Verstärker mit guten DF ist es fast wurscht was dahinter angeklemmt wird, der Verstärker verzerrt immer ähnlich - mehr steckt da wirklich nicht dahinter.

Fragen     Impressum und Haftungsausschluß