Measuring TC in the 0h to 1200h range.
Die Temperatur der Referenzspannung ist genau geregelt, trotzdem kann beobachtet werden, dass bei steigender Raumtemperatur der gemessene Spannungswert sinkt. Ursache hierfür ist eine Temperaturabhängigkeit, sehr wahrscheinlich des DUT selbst. Die Ursachen können vielfältig sein. Genau sagen läßt es sich mit Sicherheit nicht, die Ermittlung dieses TK ist die Summe aus all dieser Fehler. Dies zu untersuchen erfordert viel Zeit, ist sehr schwer und ist es bei diesem Selbstbau nicht wert.
The reference temperature is precise controlled, but a small TC can still observed. A rising room temperature results in a decreasing output voltage. It's very hard to find the exact reasons.
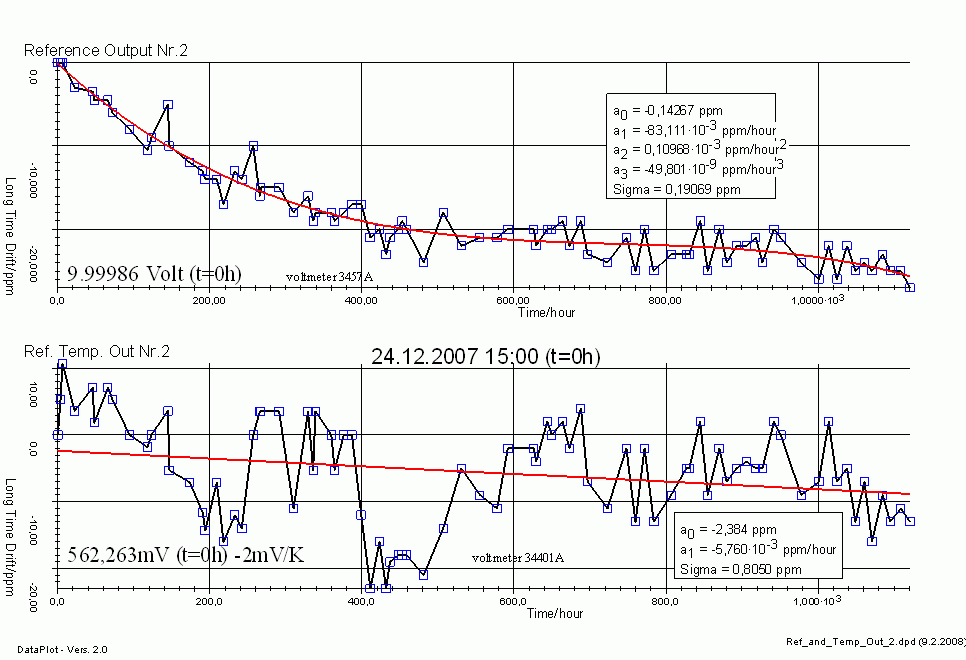
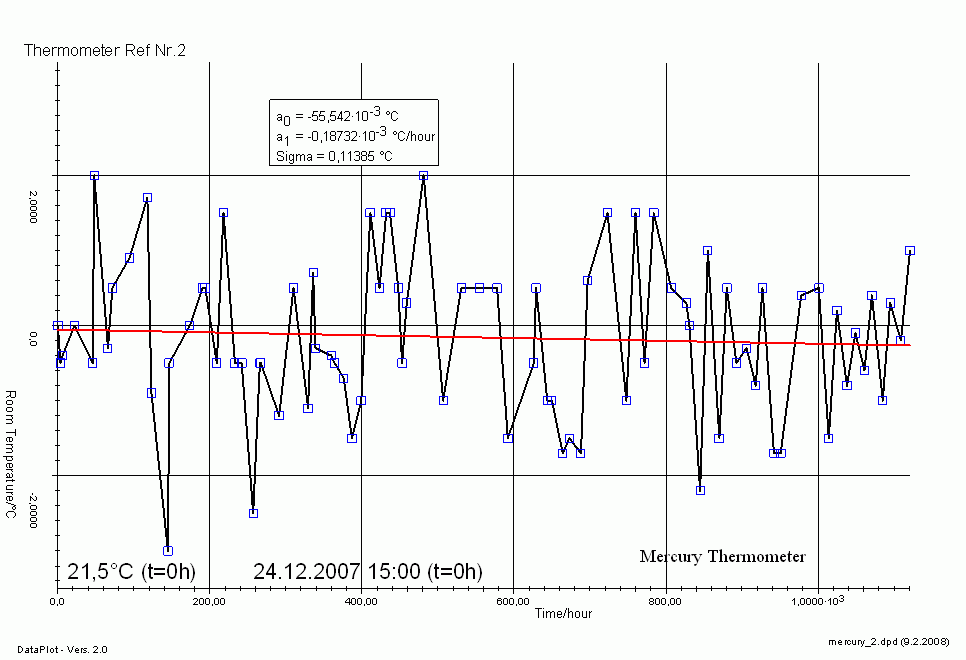
Diese Diagramme bei einem Zwischenstand von ca. 1200 Stunden werden als Datenbasis herangezogen. Man kann an signifikanten Aussreißern der Raum Temperatur ins Kalte erkennen, das dabei die Ausgangsspannungs ansteigt. Dies ist ein signifikantes Anzeichen für einen negativen Temperaturkoeffizienten.
Datplot shows 1200h. Significantly a negative temperature coefficient.
Mathematische Vorgehensweise:
aus den Messwerten der 10 Volt Ausgangsspannung läßt sich eine polynominale Regression berechnen, ein Fit der die Messwerte bestmöglich mathematisch beschreibt nach einer Wunschfunktion. Als Grundlage zur Regression wird ein Polynom dritter Ordnung herangezogen, dies erschien als sinnvolle Auswahl zur Regression. Das Polynom ist die rote Linie im Diagramm Reference Output Nr. 2
Das Polynom als Funktion der Stunden lautet:
3.rd order olynominal fit function:
Long Time Drift (hour) = -0,14267 ppm - 0,083111 ppm/hour + 0,000'10968 ppm/hour² - 0,000'000'049 ppm/hour³
(das Polynom ist nur gültig für den Bereich hour = 0 bis 1200 !!!, alles andere wäre Spekulation und vergleichbar mit einem Blick in eine große Glasmurmel)
(polynom only valid for data within 0 to 1200h, every guess far away from 1200h is a lie)
Man sieht an der Wertigkeit der Koeffizienten, die Abweichung ist hauptsächlich erster und zweiter Ordnung.
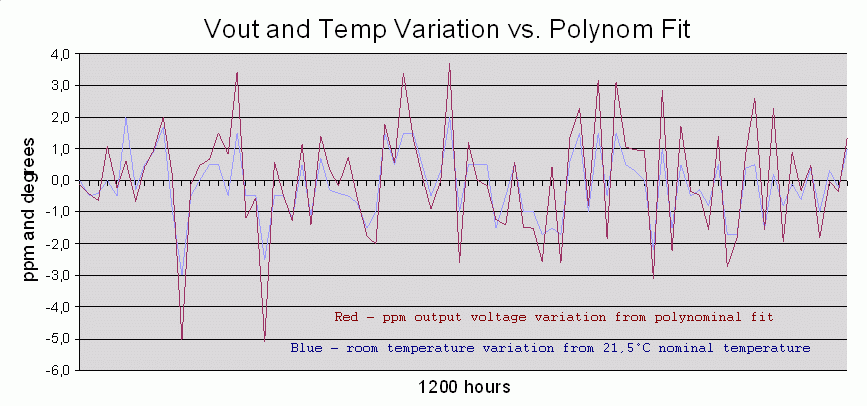
Nun berechnen wir die Differenz der gemessenen Ausgangsspannung zum Polynom Fit sowie die Differenz der Raumtemperatur zum Startwert von 21.5°C. Beide Differenzen sind aufgetragen im nächsten Diagramm. (Die Abweichung der Spannung wurde mit -1 multipliziert damit die Ausschläge beider Graphen in die gleiche Richtung verlaufen und die gleichsinnigen Ausschläge besser erkennbar sind).
Now we calculate the difference between output voltage and the fit function and second the difference between room temperature and 21.5°C. Both differences are plotted in the diagram. The voltage difference is multiplied by -1, giving a better visibility.