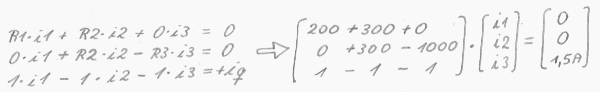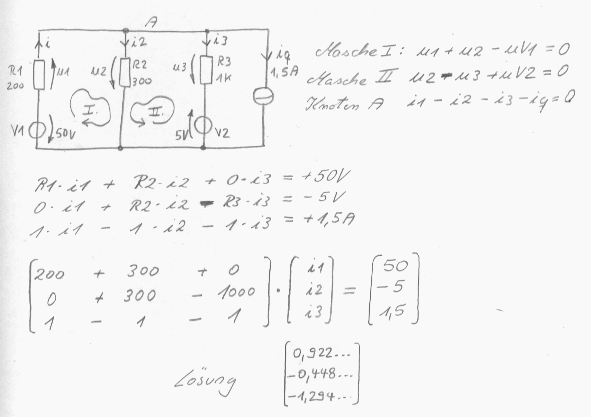Superposition - Überlagerungsmethode nach Helmholtz - Matrizen Lösung |
||||||||||||||||||||||
|
Die Überlagerungsmethode oder auch das Superpositionsprinzip ist eine weitere Methode um lineare elektrische Netzwerke zu lösen. Mit dieser Methode lassen sich auch komplizierte lineare Netzwerke vereinfachen, so daß die Lösung einfacher greifbar wird. Besonders wenn mehrere Spannungsquellen oder Stromquellen im Netzwerk vorhanden sind, ist die Verwendung dieser Methode lohnenswert. Zusätzlich zeigt der Bericht noch wie einfach mittels Matrizen und einem Rechner die Aufgaben gelöst werden können. Gegeben sei dieses Netzwerk:
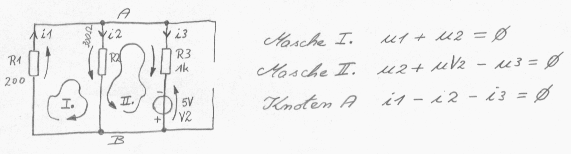
Das Netzwerk könnte nun in diesem einfachen Beispiel als Ganzes auch sofort berechnet werden nach den Knoten- und Maschenregeln; eine andere Methode in Kombiation mit der Knoten- und Maschenregel ist das Superpositionsprinzip, es kann die Berechnung von Netzwerken vereinfachen oder in manchen Fällen überhaupt erst möglich machen. Wir haben hier drei aktive Quellen, zwei Spannungsquellen und eine Stromquelle. Die Vereinfachung der Überlagerungsmethode basiert auf einer Vereinfachung des Netzwerkes, in dem zunächst nur eine einzelne Quelle betrachtet wird und alle anderen Quellen unbeachtet bleiben. In den einzelnen Zweigen des Netzwerks ist der jeweilige tatsächlich fließende Strom die algebraische vorzeichenbewerte Summe aller Einzelströme verusacht durch die jeweilige Quelle, wobei dabei alle nichtbeteiligten Quellen in der jeweiligen Einzelbetrachtung entsprechend abzuschalten sind. Es sind insgesamt drei Spannungs- oder Stromquellen, somit sind drei verschiedene Rechnungen durchzuführen: Berechnung 1:
In der Schaltung aus Bild 2 können nun die Knoten- und Maschenregeln angewandt werden. Bitte nicht erschrecken über die Fülle, es ist extra sehr ausführlich beschrieben.
Masche I: Ur2-Uv1+Ur1=0 Masche II: Ur2-Ur3=0 Knoten A: i1-i2-i3=0 Die drei Gleichungen sind nach den Strömen zu lösen, dazu gibt es mehrere Methoden, die einfachste bei dem kleinen Netzwerk ist natürlich die gedanklicher Art:
das war gerechnet in "Prosa". Falls alle Widerstände bekannt sind, geht es auch in Matrizenform, dazu werden die Knoten und Maschengleichungen untereinander geschrieben und jeder Strom bekommte eine eigene Spalte, siehe selbst wie das Schema geht, die Gleichungen sind dabei zuerst zu ordnen und Spannungen dabei durch das Produkt aus Widerstand und jeweiligem Strom zu ersetzen : R1*i1 + R2*i2 + 0*i3 = 50V 0*i1 + R2*i2 - R3*i3 = 0V 1*i1 - 1* i2 - 1*i3 = 0A Bist Du damit einverstanden, daß diese Maschen und Knoten mathematisch immer noch die gleichen sind wie oben in rosa Farbe? Sieht zwar kompliziert aus, die Ströme sind aber nun in Spalten geordnet, rechts vom Gleichheitszeichen stehen die bekannten konstanten Größen, das gilt natürlich auch für die 0, ist ja auch bekannt und konstant. Nun basteln wir das um in Matrizenform:
habe es nochmal hingeschrieben, rechts vom Pfeil steht das Gleichungssystem jetzt in Matrizenform. Das kann man selbstverständlich auch von Hand lösen über die Gaußsche Normalform GNF, auf die die Matrize per Zeilenumformungen zu bringen ist, das lassen ich sein und nehme einen etwas komfortableren Taschenrechner, der Bericht beschreibt das Superpositionsprinzip, nicht den Lösungsweg der GNF. In der großen Matrize stehen nur bekannte konstante Größen, in der ganz rechten stehen auch nur bekannte und konstant Größen, die Matrize mit den Strömen ist die Unbekannte nach der wir jetzt suchen. Man tippt die Matrizengleichung ein in den Taschenrechner am Beispiel des Hewlett Packard HP 48G:
Schwupp die wupp schon steht das Ergebnis für die gesuchte Matrix der Ströme im Taschenrechner, die oberste Zahl ist i1, Mitte i2 und die ganz unten i3. i1=0,116071428....Ampere i2=0,08928571....Ampere i3=0,02678571....Ampere Ströme erscheinen selbstverständlich mit richtigem Vorzeichen, man muß nur die zu Anfang festgelegte Richtung des Strompfeiles beachten und darf diese im Verlauf nicht mehr ändern, dann stimmt alles automatisch, in diesem Fall haben wir nur positive Ströme als Ergebnis. Für was all diesen scheinbaren Aufwand?, ganz einfach: mach mal die Methode "Prosa" bei 5 Spannungsquellen, 3 Stromquellen und 22 Widerständen - viel Spaß sag ich da nur. Mit den mathematischen Methoden ist das alles nur ein akribisches Aufstellen der Knoten- und Maschengleichungen, das Berechnen kann dann ein Rechner übernehmen. Viele scheinbar sehr komplizierte Aufgaben reduzieren sich mit solchen Methoden auf den Level vom Rasenmähen am Samstag Nachmittag. Die Intelligenz liegt hier nicht primär in der Durchführung der Mathematik, die Intelligenz soll liegen im "Sehen und Verstehen" der Knoten und Maschen, später dann auch im echten Leben. Manche meiner frühen Lehrkräfte sahen das einst ein wenig anders und machten Schüler wild mit schwer nachvollziehbaren Prosa Zusammenfassungen (das bis zu einem gewissen Level schneller ist) mit ihren alljährlich gleichen Aufgaben an der Tafel und waren gelegentlich sehr stolz darauf die Methode Prosa besser zu können als die auf den Bänken. Ich hatte genau deswegen einst einen tierischen Haß. In meiner Studienzeit hingegen hatte ich das Glück von Professoren belehrt zu werden, die ausführlich die Methoden schulten und intensiv lehrten nach den physikalischen Gesetzen zu denken, dazu gehören eben auch das "Sehen und Verstehen" der Knoten und Maschen, dem bin ich dankbar bis heute. Berechnung 2: Aus Bild 1 superpositionieren wir nun die Spannungsquelle V2.
Wir geben ein im Taschenrechner. Diesmal beginnen wir aber mit der Eingabe der Matrix ganz rechts.
Als Ergebnis erhalten wir: i1 = 0,0026785....Ampere i2 = -0,001785.......Ampere i3 = 0,0044642......Ampere (Hinweis: wenn man diese langen Zahlen in der Matrix auf dem Display nicht mehr sehen kann, dann Shift Rosa_View drücken und mit den Pfeiltasten toggeln.) Berechnung 3: Aus Bild 1 superpositionieren wir nun die Stromquelle I1.
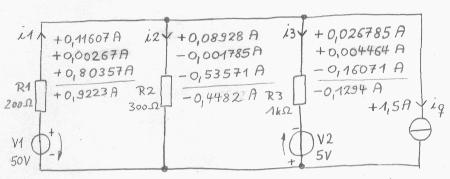
Der Taschenrechner liefert wieder die Lösungsmatrize für i1, i2 und i3: i1 = 0,8035714......Ampere i2 = -0,535714......Ampere i3 = -0,160714.......Ampere Berechnung des Gesamtergebnisses: Aus den drei verschiedenen Lösungmatrizen erhalten wir nun das Gesamtergebnis, in dem wir diese drei Matrizen einfach zusammen addieren. Das Ergebnis sind die Ströme für i1, i2 und i3, wenn in der Schaltung alle Spannungsquellen und die Stromquelle aktiv sind. i1 = 0,9223214.......Ampere i2 = -0,448214........Ampere i3 = -0,129464.......Ampere
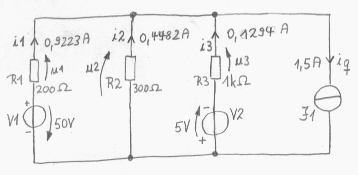
Natürlich sollte man das Ergebnis nicht so häßlich stehen lassen, die Vereinfachung ist jetzt aber leicht:
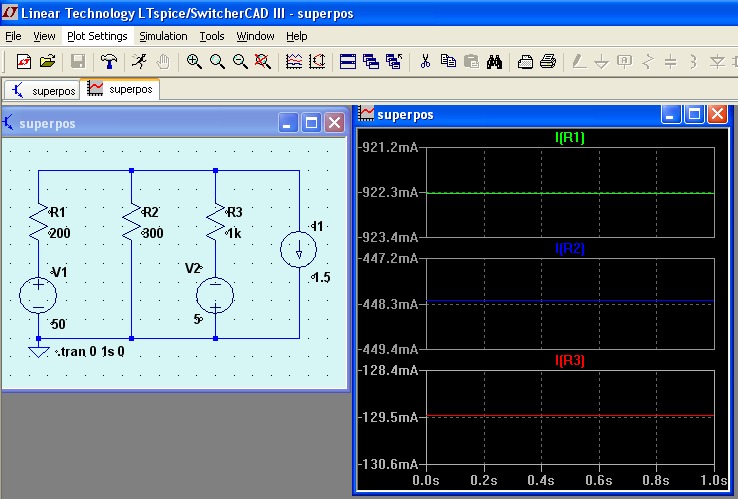
Überprüfung mit Simulationsprogramm:
Anzumerken ist noch bei nicht idealen Spannungsquellen, die einen Innenwiderstand aufweisen, für das Superpositionsprinzip muss der Innenwiderstand der Spannungsquelle nach außen in die Schaltung verlagert werden, er darf nicht mit ausgebaut werden. Genauso bei nicht idealen Stromquellen, der hohe Parallelwiderstand muß in der Schaltung verbleiben. Innenwiderstände der Quellen sind daher wie externe Widerstände zu betrachten. Das Superpositionsverfahren ist einfach, die Widerstände müssen bekannt sein, sind sie es nicht, so sind sie nach Möglichkeit auf die verschiedensten zuerst zu berechen, so viele Freiheitsgrade muss die Aufgabe hergeben. Die Gefahrenquelle an Fehlern liegt in Vorzeichenfehlern, das passiert sehr schnell - an diesen Stellen muss man höllisch aufpassen, besonders auch beim Aufstellen der Maschen- und Knotengleichungen. Das Lösen der Aufgabe mittels Matrizen ist nur ein Weg von mehreren um an die Lösung zu gelangen. Die obige Aufgabe läßt sich auch ohne Superposition gleich mit Hilfe der Matrizen lösen, sie ist zur Darstellung der Überlagerung jedoch gut geeignet gewesen:
einfacher als diese Methode mittels Matrizen geht es wohl kaum noch? Außer dem Superpositionsprinzip gibt es noch weitere Methoden wie das Maschenstromverfahren nach Maxwell sowie die Methode Ersatzstromquelle und Ersatzspannungsquelle, das aber ein anderes Mal, es war bereits viel Arbeit das obige Verfahren anschaulich zu erklären. Mit der Zeit entwickelt man ein Gefühl dafür, welche Methode ein geeigneter Lösungsansatz ist, darin liegt auch die Kunst, das Rechnen selbst ist nicht so schwer. Die ganzen Verfahren werden im Grundstudium zur Elektrotechnik gelehrt.
|
||||||||||||||||||||||
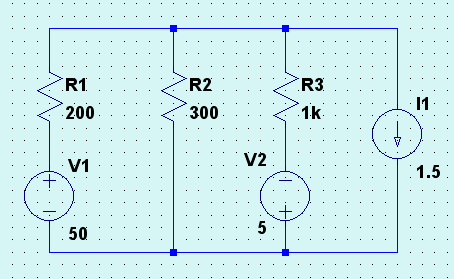
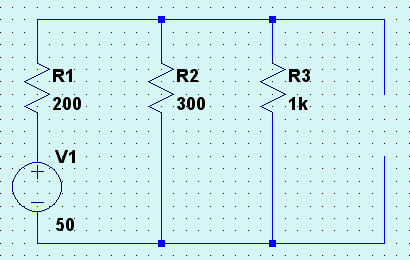
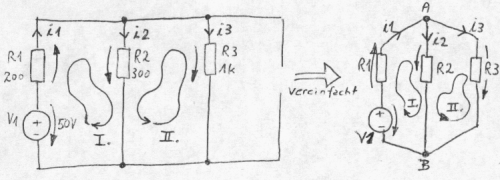
 Bild 4:
Bild 4: