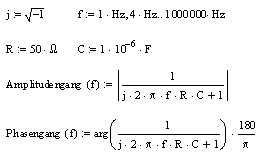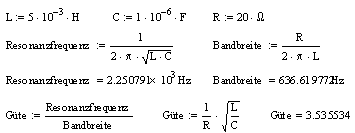|
Ein Tiefpass ist nichts anderes
als ein einfacher Spannungsteiler. Er
enthält anstatt rein ohmscher Widerstände auch Bauteile, die einen
frequenzabhängigen, daher auch genannt "komplexen" Widerstand aufweisen.
Dies können Kondensatoren und/oder Induktivitäten sein. Ein Tiefpass hat
mindestens einen Energiespeicher, dies kann wiederum entweder ein
Kondensator oder eine Induktivität sein. Hat er mehr als einen
nennenswerten Energiespeicher so spricht man von einem Tiefpass höherer
Ordnung, bei zwei Energiespeichern nennt man dies zweiter Ordnung, bei drei dritter
Ordnung usw.
In der Realität sind Tiefpässe
rein erster Ordnung nicht realisierbar, parasitäre Elemente sorgen immer für
höhere Ordnungen, auch reines Tiefpassverhalten gibt es in der Realität nicht, ab
irgendwelchen Frequenzbereichen können die Verhältnisse sich stark
verändern oder gar umkehren. Was ich damit sagen will ist, das gewünschte
Verhalten ist sehr oft gut definiert für die betrachteten Frequenzbereiche, in
diesen läßt sich auch erste Ordnung realisieren, aber nur da wo der
eine Energiespeicher dominant ist.
Tiefpass Filter bedeutet die
tiefen Frequenzanteile passieren den Filter, die höheren werden mehr oder
weniger stark gedämpft. Tiefpässe sind in der Elektrotechnik überall anzutreffen, bspw. Glättungskondensatoren nach einem
Brückengleichrichter, Eingangsfilter an Verstärkereingängen, Power Supply
Bypass Kondensatoren an IC's und Operationsverstärkern um nur ein paar
populäre Anwendungen zu nennen.
|
Außerhalb der
Elektrotechnik könnten auch dies Tiefpässe sein:
-
mach mal schön langsam.
-
nur keine Hektik, mich interessieren nur konstantere Dinge.
-
wenn's im Winter nur einen Tag
Frost hat, friert der See noch lange nicht ein.
-
nur einen Tag lang deinen
Schotter zu sparen bringt nicht viel, genauso wenig wie einen Tag über
deine Verhältnisse gelebt dich nicht arm macht (normalerweise zumindest,
es sei denn etwas extremes passiert, z.B. du heiratest die falsche Frau
in einem Lande mit merkwürdiger Rechtssprechung).
-
Ein Tiefpass hat ein integrierendes, ein auf Systeme beruhigendes,
verzögerndes Verhalten.
|
Der am häufigsten angewandte Tiefpass besteht aus
einem Widerstand in Reihe mit einem Kondensator und soll im weiteren näher
untersucht werden.
Numerische Berechnung mit einem Simulationsprogramm
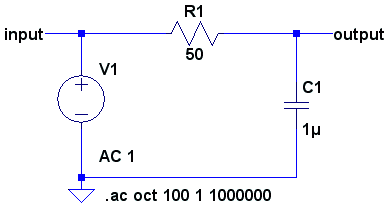 |
Das Bild
zeigt einen Tiefpaß erster Ordnung aus einem Widerstand und einen
Energiespeicher, einem Kondensator. Der Schaltplan und die
Simulation erfolgte mit dem kostenlosen Simulationsprogramm Switcher
Cad 3 von www.linear.com
Es wird
mit dem Programm zunächst eine AC Analyse durchgeführt. An der
Spannungsquelle V1 wird eine sinusförmige Wechselspannungsamplitude
von 1 Volt eingestellt. Die Frequenz verändert sich von 1 Hertz bis
auf 1 MHz. In kleinen Frequenzschritten wird diese nun erhöht und
jeweils dafür die Spannungen in der Schaltung berechnet.
|
|
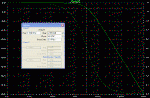 |
die
Simulation zeigt nun das Bodediagramm der Ausgangsspannung "output"
des Tiefpass. Ein Bodediagramm bezeichnet den Amplitudengang zusammen
mit dem Phasengang. Es zeigt wie Amplitude und Phase zusammen mit
der Frequenz "gehen". Die durchgezogene Linie ist der
Amplitudengang, die gestrichelte Line der Phasengang. Zur besseren
Darstellung eines weiten Zahlenbereiches wurde eine doppelt logarythmische Darstellung gewählt, sowohl
in der Frequenz- als auch
in der Amplitudenachse, die Skala für die Phasenverschiebung ist linear. |
Ein in der Terminologie der
Elektrotechnik bedeutender Punkt bei dieser Tiefpassbetrachtung ist der
Punkt der Bandbreite oder Grenzfrequenz in der Filtersprache. Im
gezeigten Beispiel liegt er geschätzt bei etwa 3,169 kHz. Bei dieser Frequenz fällt
die Spannung am Ausgang um -3 Dezibel ab. Der Cursor kennzeichnet diesen
Punkt relativ genau. Bei der doppelt logarythmischen Darstellung fällt
dieser Punkt ins Auge als der Knickpunkt, an der der Amplitudengang
deutlich zu fallen beginnt. Die Amplitude im Tiefpass erster Ordnung fällt
nach dem Punkt der Bandbreite mit einer Steilheilt von -20
dB/Frequenzdekade. Am Beispiel der 100 kHz/-30dB und den 1 MHz/-50dB ist
das schön zu beobachten. Auch merkenswert ist zu wissen, nach der
Genzfrequenz, fällt die Amplitude pro Oktave um -6,02dB wobei eine Okatave
eine Frequenzverdoppelung ist. Im Diagramm gut zu sehen bei 100 kHz/-30dB
und 200 kHz/-36dB.
Bedeutung hat auch die
Phasenverschiebung zwischen Ausgangs- und Eingangssignal, sie verläuft von
DC Signalen und bei niedrigen Frequenzen sehr nahe
Null Grad. Dann beginnt sie rasch zu fallen und hat im Punkt der -3 dB
Bandbreite exakt -45.000... Grad, für noch höhere Frequenzen läuft sie
asymptotisch gegen minus 90 Grad, wird diese -90 Grad aber niemals
erreichen sondern ihr nur unendlich nahe kommen, so gilt das zumindest in
der Theorie für erste Ordnung, in der Praxis gibt es das natürlich nicht,
somit wird sie die -90 Grad überschreiten, die asymptotische Aussage hat
daher nur akademischen Charakter.
|
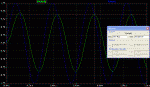 |
Die Simulation zeigt das
Zeitsignal der Eingangsspannung in Blau von 1 Volt Amplitude bei der
Grenzfrequenz von ca. 3,169 kHz. Dazugehörig die Ausgangsspannung in
Grün mit einer Amplitude von etwa 0,707 Volt (-3dB) bei natürlich
auch 3,169 kHz. Ein Tiefpass mit streng linearen idealen
Widerständen und Kondensatoren fügt keine neuen Frequenzanteile
hinzu. Besonders auffallend ist, daß das Ausgangssignal bei Beginn
der Simulation nicht sinusförmig einschwingt ! - das ist korrekt so.
Dieses Ausgangssignal ist erst nach etwa 1-2 ms eingeschwungen.
Eine
analytische komplexe Rechnung gilt daher nur für eingeschwungene
Sinussignale, das ist ganz wichtig und immer zu beachten. Sollen
auch die Einschwingvorgänge berechnet werden, können zur Berechnung
Differentialgleichungen herangezogen werden oder wie im Beispiel die
numerische Berechnung hier mittels Simulationsprogramm. |
Komplexe Berechnung
|
 |
Für eine komplexe Rechnung ist es sinnvoll die Übertragungsfunktion des
Tiefpass für eingeschwungene sinusförmige Signale zu berechnen. Die Übertragungsfunktion ist eine wichtige
Gleichung für viele regelungstechnische Systeme, wie aktive und
passive Filter oder auch Verstärker. Die Übertragungsfunktion ist
das Verhältnis aus Ausgangsgröße zu Eingangsgröße. In diesem Fall
hier das Verhältnis Ausgangsspannung Uout zu Eingangsspannung Uin.
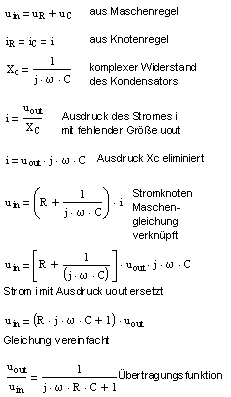
Die linke Seite zeigt wie
auf Basis der Maschenregel und der
Knotenregel die Übertragungsfunktion
dieses Netzwerkes Tiefpass erster Ordnung hergeleitet werden kann.
-
Die oberste Zeile ergibt
sich aus der einzigen in diesem Netzwerk vorhandenen Kernmasche
-
Die zweite Zeile zeigt die
Schaltung hat nur einen Stromknoten, daß bedeuted hier alle
Bauelemente befinden sich in Reihenschaltung und werden daher vom
gleichen Strom durchflossen
-
Die dritte Zeile
beschreibt den komplexen Widerstand Xc des Kondensators, dieser
ist umgekehrt proportional zur Kreisfrequenz Omega (2pi) und der
Frequenz f, wobei Omega=2pi*f ist. Der Buchstabe kennzeichnet die
imaginäre Einheit, j steht hier für die zweite Wurzel aus -1
-
Die vierte Zeile verknüpt
den Strom i mit der Größe uout das gleich der Kondensatorspannung
ist
-
Die fünfte Zeile ersetzt
den unerwünschten Ausdruck Xc
-
Die sechste Zeile
verknüpft die Strom mit der Maschengleichung
-
Die siebte Zeile
eliminiert den Strom aus dem Gleichungssystem
-
Die achte Zeile ist die
vereinfachte siebte
-
Die neunte Zeile ist die
gesuchte komplexe Übertragungsfunktion
|
|
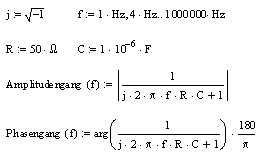 |
Mit Hilfe der komplexen Übertragungsfunktion kann nun der
Amplitudengang als auch der Phasengang dargestellt werden.
-
die oberste Zeile definiert
die imaginäre Einheit j=zweite Wurzel aus -1 und den grafisch
dargestellten Frequenzbereich von 1 Hz bis 1 MHz, sowie die
Schrittweite 4 Hz.
-
die zweite Zeile definiert
die Variable R=50 Ohm und C=1 Mikrofarad
-
die dritte Zeile ist die
Gleichung für den Amplitudengang, der Absolutbetrag der komplexen
Übertragungsfunktion
-
die vierte Zeile ist die
Gleichung für den Phasengang, das Argument (Winkel) der komplexen
Übertragungsfunktion, hier gewandelt in die 360 Grad Darstellung
mittels 180/pi.
Dem ungeübten Leser sei hier
dringend empfohlen sich mit den Grundlagen der komplexen
Zahlen zu beschäftigen, Bücher dazu gibt es im Bereich Mathematik
und Ingenieurwissenschaften sehr viele. Nach Kenntnis
derer ist es angeraten in Fachbücher der Regelungstechnik
einzusteigen. |
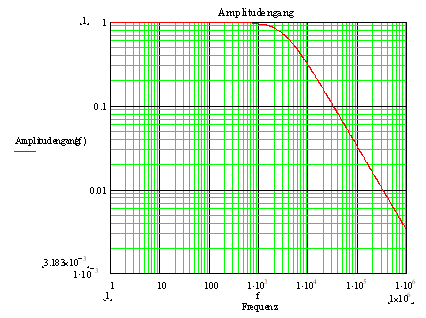
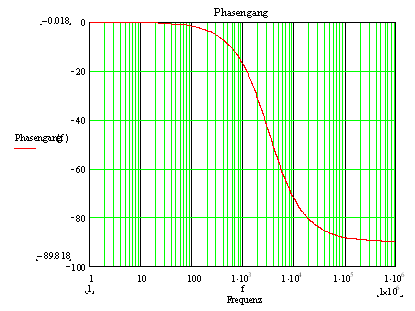
Zeigt die grafische Darstellung des
Amplitudengang und des Phasengang des Tiefpass. Die Kurven sehen gleich aus
wie in der Simulation.
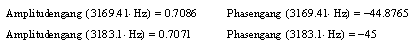
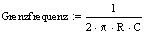 |
die
Ergebnisse sind identisch zur numerischen Simulation, genau
gerechnet liegt die Grenzfrequenz bei 3183.1 Hertz. Bei der
Grenzfrequenz sinkt die Amplitude am Ausgang auf das 0,7071 fache
(1/Wurzel2)
und die Phasenverschiebung beträgt exakt -45,000000.... Grad. |
Wohlgemerkt und nochmals zur
Erinnerung, die komplexe Rechnung ist nur gültig für stationäre
sinusförmige Signale im eingeschwungenen Zustand, sich diesen
Satz jedesmal aufs neue klar zu machen ist sehr wichtig. Genau genommen
ist die komplexe Lösung eine Lösung, die sich aus der Differentialrechnung
ergibt.
Lösung mit
Differentialgleichungsansatz:
|
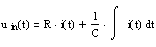 |
Solch
eine Differentialgleichung ist noch einfach zu lösen, damit können
beliebige Eingangssignale untersucht werden. Lösungswege und Bücher
über diese Mathematik existieren ettliche. Allerdings aus
praktischer Sicht, ab einer gewissen Ordnung oder wenn noch
nichtlineare Terme hinzu kommen, sind sie nicht mehr analytisch
lösbar. Selbst die gern zur Hilfe genommene La Place Transformation
stößt an ihre Grenzen, sie ist hilfreich beim Berechnen, man wird
aber spätestens feststellen bei der Rücktransformation in den
Zeitbereich geht einem oft schon wieder die Luft aus. |
Eine Berechnungsmöglichkeit bei
Filtern höherer Ordnung ist die komplexe Rechnung und sich auf
eingeschwungene sinusförmige Signale zu beschränken. Allerdings kann auch
bei komplexer Rechnung und höherer Ordnung, sich diese Berechnung zu
ziemlichen Rechenwerken ausweiten, der besondere Nutzen liegt dann darin
funktionelle Abhängigkeiten von Variablen zu erkennen. Kommen jedoch
nichtlineare Effekte hinzu ist auch die komplexe Rechnung am Ende. Für
solche Fälle ist nur noch die numerische Mathematik z.B. per Simulation
hilfreich. Neben den vielen Vorteilen wie Einfachheit und Zeitersparnis
ist es ein Nachteil der Simulation, daß gerade diese expliziten
Abhängigkeiten von Variablen nicht im Detail als Gleichung erkennbar sind.
Beide Methoden zu nutzen ist meistens der sinnvollste Weg.
Tiefpass zweiter Ordnung
|
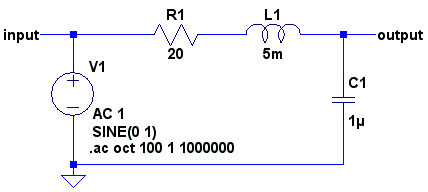 |
Ein Tiefpass zweiter Ordnung, er hat nun zwei
Energiespeicher, den Kondensator C1 und die Induktivität L1. Durch
den zusätzlichen Energiespeicher wird der Tiefpass in seiner Wirkung
stärker, auch die Phasenverschiebung zwischen Eingang und Ausgang
erhöht sich.
Der Tiefpass könnte auch ohne den Widerstand R1
aufgebaut werden, es wäre ungedämpfter Tiefpass zweiter Ordnung. |
|
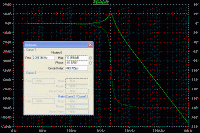 |
zeigt die
Simulation des Tiefpass zweiter Ordnung, sofort sichtbar die
Überhöhung bei ca. 2,2 kHz. Die Spannung steigt hier tatsächlich
über die Eingangsspannung an. Die Phasenverschiebung verläuft nun
sogar bis minus 180 Grad. Der Amplitudenabfall beträgt nun
-40dB/Dekade oder -12dB/Oktave.
Abhängig
vom Serienwiderstand R1 bestimmt sich die Güte dieses
Serienschwingkreises und damit die Höhe des Überschwingers. |
|
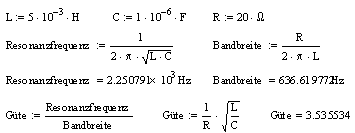 |
Ein paar
Gleichungen passend zu diesem Tiefpass.
-
Die Güte ist Maß für die Überhöhung der
Ausgangsamplitude am Punkt der Resonanzfrequenz. Die im Diagramm
abgelesene Magnitude ca. 11,05 dB das entspricht etwa 3,57fache
Überhöhung, das ist fast identisch zur berechneten Güte von 3,53.
-
Die Resonanzfrequenz
berechnet 2,25 kHz - im Diagramm abgelesen 2,204 kHz.
-
Die Bandbreite ist hier
definiert als beidseitiger Frequenzbereich um die Erhöhung herum, an
deren Flanken die Amplitude bezogen auf das Maximum um -3 dB
abgefallen ist.
|
Von praktischer Bedeutung ist die
Auswirkung der gewollten oder auch parasitären Induktivität, die in
manchen Tiefpässen ohne ausreichend dämpfendes R, gern zu unerwünschten
Überhöhungen führen kann, Power Supply Bypassing ist dazu ein besonders
kritisches Thema.
Auch die Übertragungsfunktion des
Tiefpaß zweiter Ordnung läßt sich komplex herleiten.
|