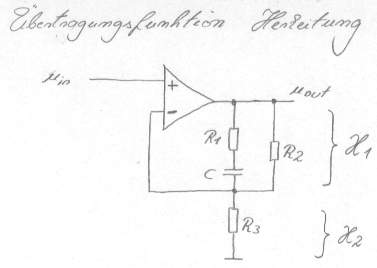
Bild 1: die Schaltung hat eine nichtinvertierende Verstärkung, besitzt je eine Polstelle und eine Nullstelle.
X1 umfasst den Teil vom Ausgang bis zum invertierenden Eingang, X2 umfasst immer den Teil vom invertierenden Anschluß bis zur Masse.
Bei einem idealen
Operationsverstärker darf nach diesen Gleichungen gerechnet werden. Diese
Gleichungen gelten nur einfach gegengekoppelte Verstärker, die auf der Basis
des zur Hilfe genommenen regelungstechnischen Ersatzschaltbildes ruhen, ein
nicht gegengekoppelter Verstärker ist eine Steuerung und keine Regelung,
diese Gleichungen gelten für ihn nicht.
Ausnahmen von diesen Regeln:
Diese Grundgleichungen sind nicht anwendbar für alle Filterschaltungen, spätestens dann wenn man vor so einer Schaltung sitzt wird man sehen, daß man mit dem Hilfsmittel Gain=1+(X1/X2) oder Gain=-X1/X2 nicht mehr weiterkommt, aber auch hier gibt es natürlich Ansätze um an die Übertragungsfunktion zu gelangen, das Aufstellen der Knoten- und Maschengleichungen unter Einbindung der der Eingänge des OP ins Ersatzschaltbild. Für diese Knoten wird dann ein Strom von 0 Ampere in die Eingänge angenommen und der Spannungsabfall zwischen dem invertierendem und nicht invertierendem Eingang zu 0 Volt gesetzt. Rechnerisch wäre der ideale OP damit erfüllt. Dieses Verfahren liefert dann auch einen Rohling für die Übertragungsfunktion, die dann im hier gezeigten Verfahren genauso weiter behandelt werden kann um an die Pol- und Nullstellen in komfortabler Darstellung zu gelangen, was ja unsere generelle Zielsetzung in diesem Bericht ist. Diese "komfortable Darstellung" der Übertragungsfunktion wie ich sie hier bename, hat den Vorteil, daß man auf einen Blick sieht und sich geistig schon vorstellen kann wie der Frequenzverlauf in etwa verläuft ohne irgendeinen Graphen berechnen zu müssen. Bei höhren Ordnungen ist jedoch mathematische Flexibilität vorteilhaft und das Schema F funktioniert zunehmend weniger.
Bei Netzwerken höherer Ordnung: es wird ruck-zuck kompliziert, selbst noch scheinbar einfache aussehende Schaltungen werden zu Biestern. Mit den Knoten- und Maschengleichungen gelangt man auch bei Netzwerken höherer Ordnung (z.B. Tief- Hochpässe mit Mehrfachmitkopplung, Sallen-Key Netzwerke, Bandpässe, Allpässe usw.) immer ans Ziel die Übertragungsfunktion herzuleiten. Nachdem es endlich geschafft hat und diese längerer mühsehliger Gleichungsumstellerei ein Ende hat ist man zur gesuchten Übertragungsfunktion gelangt. Allerdings sieht diese Übertragungsfunktion alles andere als schön aus, zu Deutsch "gräßlich bis häßlich"., da können schon für einfache Schaltungen ein paar Seiten Papier dabei herauskommen. Probiert es ruhig mal selber aus, z.B. ein mehrfachmitgekoppeltes Tiefpaßfilter.
Betrachtet man die endlich gefundene gräßliche Gleichung etwas länger uind sortiert nach j*2*pi*f Koeffizienten, ist in diesen oft eine quadratische Gleichung oder noch höher zu erkennen, oft sogar im Zähler und im Nenner. Diese sind zu lösen, um die Pole und Nullstellen isoliert "komfortabel" mit klar erkennbarer Zeitkonstante betrachten zu können. Wie gesagt von Hand und zu Fuß sind das absolut widerliche Strafarbeiten der übelsten Sorte, wenn man nicht gerade in Übung ist kann sowas den ganzen Nachmittag dauern und man hat am Ende doch einen Fehler gemacht und ein Indizies vertauscht.
Auch die meisten Lehrbücher zeigen selten (kenne keines das es im Detail vorrechnet), wie häßlich die Rechnungen hierfür sein können, es kommt oft nur berühmte Satz z.B. : "aus dieser Schaltung läßt sich folgende Gleichung herleiten", das nützt dem Änfanger meistens überhaupt nichts. Den Weg um ans Ziel zu dahin zu gelangen, dieses aufzuzeigen, es drücken sich alle herum auch viele Autoren. Gern schreibt einer vom anderen die Ergebnisse ab, die einst in der rechnerlosen Vergangenheit jemand mühselig herleitete. Ich bin auch nicht besser in der Beziehung, aber ich gib's wenigstens zu. Gelegentlich übe ich mit diesen Gleichungsmonstern manchmal klappt's manchmal auch gar nicht.
Für solche komplizierteren Netzwerke gibt es natürlich auch leichtere Lösungsmethoden, z.B: ein symboliktaugliches Mathematikprogramm wie MathCad, damit lassen sich Gleichungen beliebig umstellen und auch die komplexen Übertragungsfunktionen recht komfortabel darstellen. Übrigens solche Netzwerke höherer Ordnung sind zwar theoretisch schöne Werke der Mathematik, für richtig anspruchsvolle Schaltungen in der Praxis nach meiner Ansicht meist untauglich. Oft ist z.B. zur Realisierung irgendeine ungünstige Bedingung einzuhalten was die OP Beschaltung betrifft, z.B. ein hochohmiger Widerstand vor den OP Eingängen, und schon rauscht's heftig, was nützt mir dann die zweite Ordnung nur um einen OP zu sparen?. Mir ist es die OP Sparerei nicht wert, z.B. zwei, drei einfachere Netzwerke in Reihe erfüllen genau den selben Zweck, haben aber meist den Vorteil der individuelleren Einstellbarkeit, die erste Stufe kann beispielssweise rauschoptimiert die Spannung hochverstärke, die zweite z.B. verwendet einen OP mit höherem Ausgangsstrom usw. je nach Zielrichtung ist man so deutlich flexibler. Mit mehreren Op lassen sich z.B. auch passive LC Filternetzwerke zwischenschalten, und mit denen lassen sich ja bekanntlich auch wunderbare Funktionen erfüllen, bei richtiger Auslegung sind zudem elektrisch in manchen Punkten kaum zu schlagen.
Da Operationsverstärker mittlerweile sehr gut, klein, stromsparend und preiswert geworden sind, ist eine erhöhte Anzahl derer in meinen Augen kein Thema mehr. Noch eine Anmerkung, wer tatsächlich dazu verdonnert ist Filter achter Ordnung, einen komplizierten Allpaß oder ähnlichen Heckmeck aufzubauen, sollte sich überlegen entweder fertige Analog Filterbausteine zu verwenden oder gleich in die digitale Welt umzusteigen und die Filterfunktion einfach dort zu berechen, wenn die Geschwindigkeit hierfür ausreicht.
Bei richtig anspruchsvollen Schaltungen haben nach meiner Erfahrung diese Kunstfilter aus nur einem OP meistens keine reale Anwendung gefunden, da irgendein Parameter der Sache einen Strich durch die Rechnung gemacht hat. Auffälligerweise behandeln fast alle Lehrbücher nur die blanke Filter Theorie dazu, mir ist selten ein Werk zu Händen gekommen, das überhaupt ein anspruchsvolles praxisbezogenes Beispiel dazu parallel aufgeführt hat. Man kann diese Aussage dahinstellen wie man will, aber es ist was dran, für viele geschriebene Werke ist die Filtertheorie nur eine Möglichkeit des Protzens mathematischer Leistungen der Autoren. Der Paxisbezug läßt bis auf wenige Werke zu wünschen übrig, Ausnahmen bilden meist Werke verstorbener deutscher Professoren und Ingenieure, sie beschäftigten sich primär mit passiven Filtern oder z.B. der Kunst mit nur einer Röhre eine Klangfilterung zu realisieren. Die Hard Core Lösungen z.B. in manchen Messgeräten zur Lösung echter Herausforderungen sehen auch heute meist noch anders aus als in Standard Büchern beschrieben. Trotzdem sei diese allgemeine Literatur über Filtertechnik jedem Einsteiger dringlichst empfohlen.
Zurück zu den einfacheren Schaltungen:
Die Herleitung des Verstärkungsfaktors für einen idealen aber auch realen gegengekoppelten Verstärker mit unendlicher bzw. realer endlicher offener Schleifenverstärkung findet sich hier
Ausnahmen von diesen Regeln:
Diese Grundgleichungen sind nicht anwendbar für alle Filterschaltungen, spätestens dann wenn man vor so einer Schaltung sitzt wird man sehen, daß man mit dem Hilfsmittel Gain=1+(X1/X2) oder Gain=-X1/X2 nicht mehr weiterkommt, aber auch hier gibt es natürlich Ansätze um an die Übertragungsfunktion zu gelangen, das Aufstellen der Knoten- und Maschengleichungen unter Einbindung der der Eingänge des OP ins Ersatzschaltbild. Für diese Knoten wird dann ein Strom von 0 Ampere in die Eingänge angenommen und der Spannungsabfall zwischen dem invertierendem und nicht invertierendem Eingang zu 0 Volt gesetzt. Rechnerisch wäre der ideale OP damit erfüllt. Dieses Verfahren liefert dann auch einen Rohling für die Übertragungsfunktion, die dann im hier gezeigten Verfahren genauso weiter behandelt werden kann um an die Pol- und Nullstellen in komfortabler Darstellung zu gelangen, was ja unsere generelle Zielsetzung in diesem Bericht ist. Diese "komfortable Darstellung" der Übertragungsfunktion wie ich sie hier bename, hat den Vorteil, daß man auf einen Blick sieht und sich geistig schon vorstellen kann wie der Frequenzverlauf in etwa verläuft ohne irgendeinen Graphen berechnen zu müssen. Bei höhren Ordnungen ist jedoch mathematische Flexibilität vorteilhaft und das Schema F funktioniert zunehmend weniger.
Bei Netzwerken höherer Ordnung: es wird ruck-zuck kompliziert, selbst noch scheinbar einfache aussehende Schaltungen werden zu Biestern. Mit den Knoten- und Maschengleichungen gelangt man auch bei Netzwerken höherer Ordnung (z.B. Tief- Hochpässe mit Mehrfachmitkopplung, Sallen-Key Netzwerke, Bandpässe, Allpässe usw.) immer ans Ziel die Übertragungsfunktion herzuleiten. Nachdem es endlich geschafft hat und diese längerer mühsehliger Gleichungsumstellerei ein Ende hat ist man zur gesuchten Übertragungsfunktion gelangt. Allerdings sieht diese Übertragungsfunktion alles andere als schön aus, zu Deutsch "gräßlich bis häßlich"., da können schon für einfache Schaltungen ein paar Seiten Papier dabei herauskommen. Probiert es ruhig mal selber aus, z.B. ein mehrfachmitgekoppeltes Tiefpaßfilter.
Betrachtet man die endlich gefundene gräßliche Gleichung etwas länger uind sortiert nach j*2*pi*f Koeffizienten, ist in diesen oft eine quadratische Gleichung oder noch höher zu erkennen, oft sogar im Zähler und im Nenner. Diese sind zu lösen, um die Pole und Nullstellen isoliert "komfortabel" mit klar erkennbarer Zeitkonstante betrachten zu können. Wie gesagt von Hand und zu Fuß sind das absolut widerliche Strafarbeiten der übelsten Sorte, wenn man nicht gerade in Übung ist kann sowas den ganzen Nachmittag dauern und man hat am Ende doch einen Fehler gemacht und ein Indizies vertauscht.
Auch die meisten Lehrbücher zeigen selten (kenne keines das es im Detail vorrechnet), wie häßlich die Rechnungen hierfür sein können, es kommt oft nur berühmte Satz z.B. : "aus dieser Schaltung läßt sich folgende Gleichung herleiten", das nützt dem Änfanger meistens überhaupt nichts. Den Weg um ans Ziel zu dahin zu gelangen, dieses aufzuzeigen, es drücken sich alle herum auch viele Autoren. Gern schreibt einer vom anderen die Ergebnisse ab, die einst in der rechnerlosen Vergangenheit jemand mühselig herleitete. Ich bin auch nicht besser in der Beziehung, aber ich gib's wenigstens zu. Gelegentlich übe ich mit diesen Gleichungsmonstern manchmal klappt's manchmal auch gar nicht.
Für solche komplizierteren Netzwerke gibt es natürlich auch leichtere Lösungsmethoden, z.B: ein symboliktaugliches Mathematikprogramm wie MathCad, damit lassen sich Gleichungen beliebig umstellen und auch die komplexen Übertragungsfunktionen recht komfortabel darstellen. Übrigens solche Netzwerke höherer Ordnung sind zwar theoretisch schöne Werke der Mathematik, für richtig anspruchsvolle Schaltungen in der Praxis nach meiner Ansicht meist untauglich. Oft ist z.B. zur Realisierung irgendeine ungünstige Bedingung einzuhalten was die OP Beschaltung betrifft, z.B. ein hochohmiger Widerstand vor den OP Eingängen, und schon rauscht's heftig, was nützt mir dann die zweite Ordnung nur um einen OP zu sparen?. Mir ist es die OP Sparerei nicht wert, z.B. zwei, drei einfachere Netzwerke in Reihe erfüllen genau den selben Zweck, haben aber meist den Vorteil der individuelleren Einstellbarkeit, die erste Stufe kann beispielssweise rauschoptimiert die Spannung hochverstärke, die zweite z.B. verwendet einen OP mit höherem Ausgangsstrom usw. je nach Zielrichtung ist man so deutlich flexibler. Mit mehreren Op lassen sich z.B. auch passive LC Filternetzwerke zwischenschalten, und mit denen lassen sich ja bekanntlich auch wunderbare Funktionen erfüllen, bei richtiger Auslegung sind zudem elektrisch in manchen Punkten kaum zu schlagen.
Da Operationsverstärker mittlerweile sehr gut, klein, stromsparend und preiswert geworden sind, ist eine erhöhte Anzahl derer in meinen Augen kein Thema mehr. Noch eine Anmerkung, wer tatsächlich dazu verdonnert ist Filter achter Ordnung, einen komplizierten Allpaß oder ähnlichen Heckmeck aufzubauen, sollte sich überlegen entweder fertige Analog Filterbausteine zu verwenden oder gleich in die digitale Welt umzusteigen und die Filterfunktion einfach dort zu berechen, wenn die Geschwindigkeit hierfür ausreicht.
Bei richtig anspruchsvollen Schaltungen haben nach meiner Erfahrung diese Kunstfilter aus nur einem OP meistens keine reale Anwendung gefunden, da irgendein Parameter der Sache einen Strich durch die Rechnung gemacht hat. Auffälligerweise behandeln fast alle Lehrbücher nur die blanke Filter Theorie dazu, mir ist selten ein Werk zu Händen gekommen, das überhaupt ein anspruchsvolles praxisbezogenes Beispiel dazu parallel aufgeführt hat. Man kann diese Aussage dahinstellen wie man will, aber es ist was dran, für viele geschriebene Werke ist die Filtertheorie nur eine Möglichkeit des Protzens mathematischer Leistungen der Autoren. Der Paxisbezug läßt bis auf wenige Werke zu wünschen übrig, Ausnahmen bilden meist Werke verstorbener deutscher Professoren und Ingenieure, sie beschäftigten sich primär mit passiven Filtern oder z.B. der Kunst mit nur einer Röhre eine Klangfilterung zu realisieren. Die Hard Core Lösungen z.B. in manchen Messgeräten zur Lösung echter Herausforderungen sehen auch heute meist noch anders aus als in Standard Büchern beschrieben. Trotzdem sei diese allgemeine Literatur über Filtertechnik jedem Einsteiger dringlichst empfohlen.
Zurück zu den einfacheren Schaltungen:
Die Herleitung des Verstärkungsfaktors für einen idealen aber auch realen gegengekoppelten Verstärker mit unendlicher bzw. realer endlicher offener Schleifenverstärkung findet sich hier

Bild 2: Übertragungsfunktion mancher idealer nichtinvertierenden gegengekoppelten Verstärkerschaltungen mit unendlicher offener Schleifenverstärkung
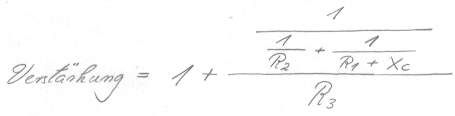
Bild 3 zeigt die komplexe Übertragungsfunktion aus den Netzwerken X1 und X2 gebildet, mit Xc=1/jwC
Die weitere Vorgehensweise ist es nun diese gefundene Gleichung soweit umzubauen, daß diese aus klar erkennbaren Pol- und Nullstellen zusammengesetzt ist. Wir wollen die komfortable Darstellung. In einer komplexen linearen Übertragungsfunktion existieren hauptsächlich drei Grundelemente:
- ein linearer frequenzunabhängiger Verstärkungsfaktor
- eine Polstelle, eine Absenkung der linearen Verstärkung beginnend in dominanter Weise ab einer charakteristischen Frequenz (-3dB Eckfrequenz) mit -20dB pro Frequenzdekade
- eine Nullstelle, ein Anstieg der linearen Verstärkung beginnend in dominanter Weise ab einer charakteristischen Frequenz (+3dB Eckfrequenz) mit +20dB pro Frequenzdekade
Diese Methode der Umformung hat sich als günstig erwiesen: nun geht es darum die Übertragungsfunktion zunächst so umzuformen, daß die gesamte Gleichung nur aus einem einzigen Bruch besteht, nur ein einziger Nenner und nur ein einziger Zähler ist das nächste Ziel.
Wir beginnen am besten mit der ersten Vereinfachung, der Eliminierung des großen störenden Doppelbruches in Bild 3 und erhalten Bild 4:
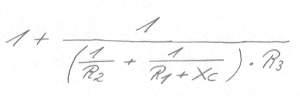
Bild 4: der große Doppelbruch wurde eliminiert und die Gleichung sieht schon angenehmer aus
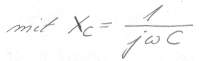
Bild 5: die komplexe Schreibweise eines Kondensators, wäre es eine Induktivität so würde dort der Kehrwert und L statt C stehen.
Der nächste Schritt (hätte man auch schon vorher machen können) ist der korrekte Übergang in die komplexe Zahlenwelt. Das Xc stand bisher als Abkürzung für den komplexen Widerstand des Kondensators. Wir wollen nun aber auch die komplexe Einheit j sowie die Kreisfrequenz Omega=2*pi*f in die Gleichung einführen. Dies durch die Substitution mit Bild 5 erledigt.
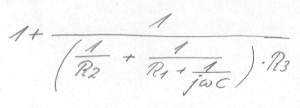
Bild 6 die komplexe Schreibweise für den Kondensator ist eingefügt
Die Gleichung kann nun weiter verarbeitet werden mit der Fortführung der Zielsetzung alle Brüche zu entfernen, als Startposition bietet sich die Position um das j herum an.

Bild 7 Hauptnenner gesucht
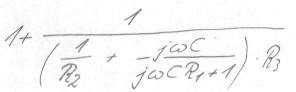
Bild 8 Bruch gestürzt (ein Bruch weniger als zuvor)
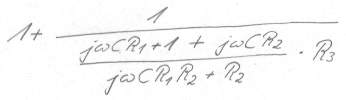
Bild 9 Hauptnenner gesucht, wieder mit der Zielsetzung die Anzahl der Brüche zu reduzieren
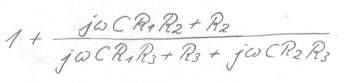
Bild 10 Bruch gestürzt (ein Bruch weniger als zuvor) gleichzeitig noch R3 einmultipliziert, damit der auch mal versorgt ist
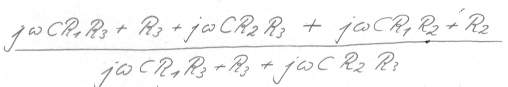
Bild 11 wieder ein Bruch weniger, diesmal diese nervige 1 eliminiert, Ziel fast erreicht
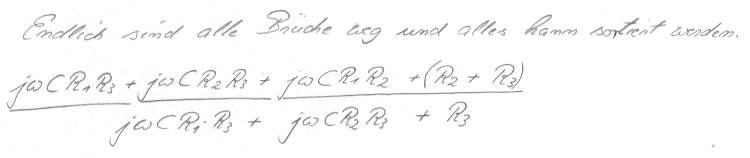
Bild 12 da nun alle eliminierbaren Brüche weg sind, konnte die Gleichung sortiert werden, damit etwas Ordnung herscht.
Man sieht hier jetzt ganz
deutlich es gibt nur noch einen Nenner und nur noch einen Zähler, diesen
Zustand zu erreichen das war das Ziel aller vorhergehenden Umformungen,
alles Schema-f ohne einmal darüber nachdenken zu müssen, was man gerade tut,
die Methode funktioniert nachts um halb 4, selbst halb betrunken.
Nun muss wieder kurz das Gehirn eingeschaltet werden und dieses Wirrwar in Bild 12 näher betrachtet werden. Auf den ersten Blick könnte man meinen das sind ja ettliche Pol- und Nullstellen, keine Angst sind es nicht. Eine Pol- oder Nullstelle eines Kondensators besteht immer aus dem Grundelement j*2*pi*f*R*C+1. Das Produkt aus R*C bildet die Zeitkonstante Tau, dieses Tau muss die Einheit "Sekunde" haben, wenn manTau multipliziert mit der Frequenz wird die Pol- bzw Nullstelle Einheitenlos. Diese Bedingung ist zwingend zu erfüllen.
In unserem Bild 12 haben wir für unser "Scheinbar Tau" die Einheiten von C*R*R, das gibt natürlich nicht die geforderte Einheit Sekunde für Tau, man sieht ganz klar, da ist noch Arbeit zu erledigen und die Gleichung so umzuformen, daß Tau die Einheit Sekunde erhält, das ist nun das erklärte Ziel der nächsten Umformung:
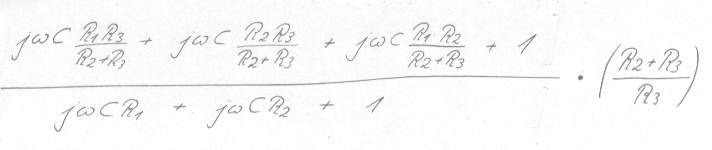
Bild 13 störender Term ist ausgeklammert worden
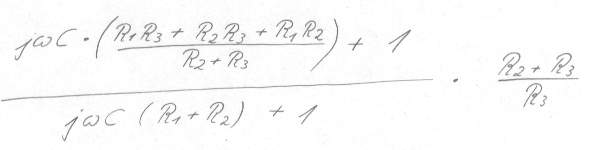
Bild 14 Gleichung lediglich umgestellt
Nun muss wieder kurz das Gehirn eingeschaltet werden und dieses Wirrwar in Bild 12 näher betrachtet werden. Auf den ersten Blick könnte man meinen das sind ja ettliche Pol- und Nullstellen, keine Angst sind es nicht. Eine Pol- oder Nullstelle eines Kondensators besteht immer aus dem Grundelement j*2*pi*f*R*C+1. Das Produkt aus R*C bildet die Zeitkonstante Tau, dieses Tau muss die Einheit "Sekunde" haben, wenn manTau multipliziert mit der Frequenz wird die Pol- bzw Nullstelle Einheitenlos. Diese Bedingung ist zwingend zu erfüllen.
In unserem Bild 12 haben wir für unser "Scheinbar Tau" die Einheiten von C*R*R, das gibt natürlich nicht die geforderte Einheit Sekunde für Tau, man sieht ganz klar, da ist noch Arbeit zu erledigen und die Gleichung so umzuformen, daß Tau die Einheit Sekunde erhält, das ist nun das erklärte Ziel der nächsten Umformung:
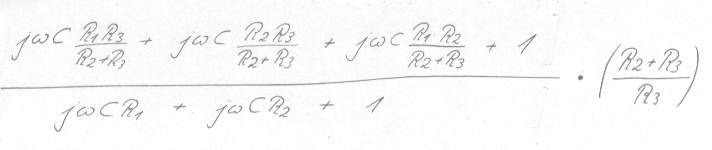
Bild 13 störender Term ist ausgeklammert worden
Jetzt musste man erstmalig ein
klein wenig denken: der Term (R2+R3)/R3 musste ausgeklammert werden damit
die wichtige Bedingung zur Erfüllung der Tau Sekunden Bedingung erfüllt ist.
Zusätzlich erschient jetzt auch die zu einer Pol- und Nullstelle zwingend
gehörende "+1". Sich auf die "+1" als Zielsetzung zu orientieren, um zu
wissen was auszuklammern ist, ist ein guter Ansatz. Wir sind fast am Ziel
angelangt.
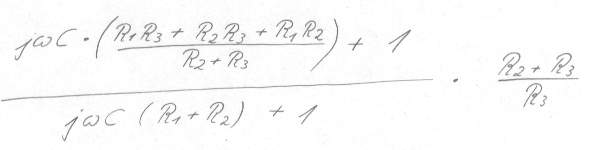
Bild 14 Gleichung lediglich umgestellt
Nun wurde die Gleichung
umgestellt. Dazu wurde jwC jeweils ausgeklammert, jetzt sieht das aus wie
eine vernüftige Pol- und Nullstelle. Was ist denn das einheitenlose
(R2+R3)/R3?, na klar der DC Verstärkungsfaktor. Trotzdem, werden wir die
Gleichung noch ein wenig schöner hinschreiben, so daß alles auf den ersten
Blick besser erkennbar wird. Die DC Verstärkung kann auch noch vereinfacht
werden.
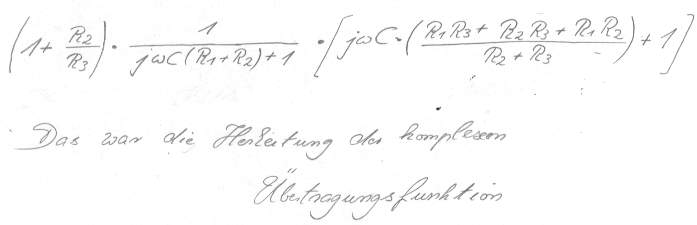
Bild 15 fertige komplexe Übertragungsfunktion
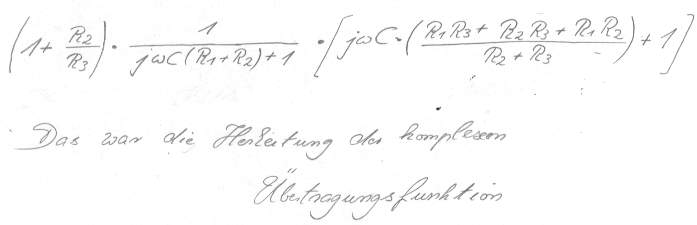
Bild 15 fertige komplexe Übertragungsfunktion
Das war alles. War doch wohl
wirklich nicht schwer oder? Ich weiß wirklich nicht warum um das Herleiten
einer Übertragungsfunktion oft ein riesen Galama veranstaltet wird und
hunderte von Übungsaufgaben dazu gemacht werden müssen - nützt doch alles
nichts - das entscheidende dafür ist den richtigen Weg ans Ziel zu kennen
und der geht zusammenfassend so:
zehn einfache Schritte:
Eines muss man zugeben, sind die Netzwerke noch etwas größer entstehen bereits wüste Apparate von Gleichungen, die sehr groß werden können. Die Möglichleit sich da zu vertun und einen Flüchtigkeitsfehler z.B. beim Umstellen einzubauen sind natürlich gegeben. Das Verfahren mit großen Netzwerken ist jedoch dasselbe. Für große Netzwerke sollte man hierfür besser ein symbolisch arbeitendes Mathematikprogramm verwenden, das einem hilft die Gleichungen ohne Flüchtigkeitsfehler richtig umzustellen.
Der nächste Schritt wäre das Wandeln der komplexen komfortablen Darstellung in die Betrags- und Phasenwinkelfunktion. Diese beiden Funktionen sind notwendig zur Darstellung von Amplituden- und Phasengang in einem gemeinsamen Diagramm, auch Bodediagramm genannt. Der Amplitudengang erfolgt üblicherweise in doppel logarithmischer Achsenskalierung (auch halblog ist manchmal sinnvoll). Der Phasengang normalerweise in Winkelgraden.
Zur Berechnung des Amplitudengang ist aus der komplexen Zahl, die die Übertragungsfunktion ja ist, der Betrag dieser komplexen Zahl zu bilden
Zur Berechnung des Phasengangs ist der arcus tangens der komplexen Übertragungsfunktion.
In der Praxis überläßt man diese Aufgabe für komplizierte Netzwerke am besten einem symbolischen Rechenknechten, der das mit einer Zeile Code erledigt. Das Diagramm kann dann problemlos geplottet werden.
Da aber die komfortable Darstellung die einzelnen Glieder mulitplikativ verbindet entspricht dies in logarithmischer Darstellung einer Addition der Pol- und Nullstellen und diese ist sehr einfach grafisch mit einem Stück Papier darstellbar. Selbst wenn für einzelne Frequenzen diskrete Amplituden- und Phasenwerte berechnet werden müssen, dazu genügt ein einfascher Taschenrechner mit komplexer Eingabemöglichkeit. Die Berechnung der Gleichungen für Amplituden- und Phasengang ist nur komplexe Mathematik, im Prinzip ist es Geometrie, darauf möchte ich hier jetzt nicht eingehen und werde dies vielleicht einmal in einem gesonderten Bericht behandeln.
um zu beweisen, daß die bisher gezeigten Methoden auch für andere Schaltungen gelten, füge ich gern noch ein anderes Beispiel hinzu. Es wird genau die empfohlene Reihenfolge eingehalten.
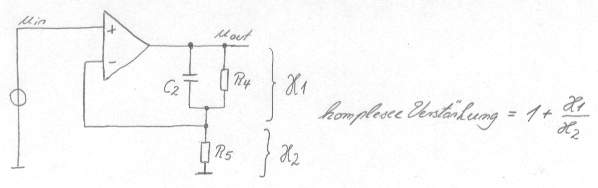
Bild 16
Schritt 1: Schaltung unterscheiden in invertierenden oder nicht invertierenden Verstärker, die jeweilige ideale Grund-Übertragungsfunktion ist anzuwenden, 1+(X1/X2) für nichtinvertierende und -X1/X2 für invertierende Schaltungen; (gelingt nicht bei allen Schaltungen). Hier ist es eine nicht invertierende Schaltung.
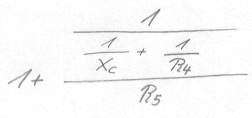
Bild 17
Schritt 2: Esatzschaltbild für X1 bilden, dabei Kondensatoren als Xc und Induktivitäten als XL behandeln
Schritt 3: Esatzschaltbild für X2 bilden, dabei Kondensatoren als Xc und Induktivitäten als XL behandeln
Schritt4: X1 und X2 in die jeweilige Grundgleichung des invertierenden oder nicht invertierenden Verstärker einsetzen.
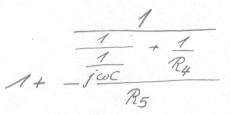
Bild 18
Schritt 5: den Übergang in die komplexe Zahlenebene durchführen, in dem Xc durch 1/jwC und XL durch jwL ersetzt werden.
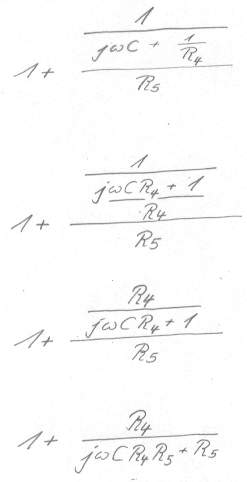
Bild 19
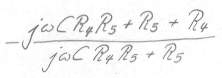
Bild 20
Schritt 6: Reduzierung der vielen Brüche auf einen einzigen verbleibenden, mit nur einem Zähler und nur einem Nenner, jede mathematische Methode hierzu sei willkommen.
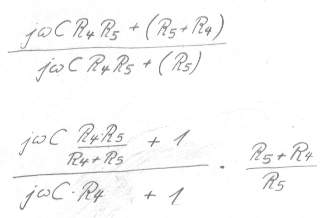
Bild 21
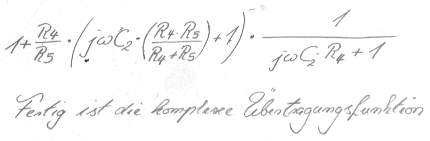
Bild 22
Schritt 10: Gleichung noch etwas aufräumen und Pol- und Nullstellen einzeln hintereinander hinschreiben.
Ist doch ganz einfach oder?
zehn einfache Schritte:
- Schaltung unterscheiden in invertierenden oder nicht invertierenden Verstärker, die jeweilige ideale Grund-Übertragungsfunktion ist anzuwenden, 1+(X1/X2) für nichtinvertierende und -X1/X2 für invertierende Schaltungen; (gelingt nicht bei allen Schaltungen).
- Ersatzschaltbild für X1 bilden, dabei Kondensatoren als Xc und Induktivitäten als XL behandeln
- Ersatzschaltbild für X2 bilden, dabei Kondensatoren als Xc und Induktivitäten als XL behandeln
- X1 und X2 in die jeweilige Grundgleichung des invertierenden oder nicht invertierenden Verstärker einsetzen.
- Den Übergang in die komplexe Zahlenebene durchführen, in dem Xc durch 1/jwC und XL durch jwL ersetzt werden.
- Reduzierung der vielen Brüche auf einen einzigen verbleibenden, mit nur einem Zähler und nur einem Nenner, jede mathematische Methode hierzu sei willkommen.
- Im Zähler wird genau der Term ausmultipliziert, der dazu führt daß alle "ScheinbarTau" Zeitkonstanten des Zählers die Einheit Sekunde bekommen. Zudem muss bei Pol-,Nulllstellen die "+1" entstehen.
- Im Nenner wird genau der Term ausmultipliziert, der dazu führt daß alle "ScheinbarTau" Zeitkonstanten des Nenners die Einheit Sekunde bekommen. Zudem muss bei Pol-, Nullstellen die "+1" entstehen.
- Vereinfachen und Ausmultiplizieren von jwC
- Gleichung noch etwas aufräumen und Pol- und Nullstellen einzeln hintereinander hinschreiben
Eines muss man zugeben, sind die Netzwerke noch etwas größer entstehen bereits wüste Apparate von Gleichungen, die sehr groß werden können. Die Möglichleit sich da zu vertun und einen Flüchtigkeitsfehler z.B. beim Umstellen einzubauen sind natürlich gegeben. Das Verfahren mit großen Netzwerken ist jedoch dasselbe. Für große Netzwerke sollte man hierfür besser ein symbolisch arbeitendes Mathematikprogramm verwenden, das einem hilft die Gleichungen ohne Flüchtigkeitsfehler richtig umzustellen.
Der nächste Schritt wäre das Wandeln der komplexen komfortablen Darstellung in die Betrags- und Phasenwinkelfunktion. Diese beiden Funktionen sind notwendig zur Darstellung von Amplituden- und Phasengang in einem gemeinsamen Diagramm, auch Bodediagramm genannt. Der Amplitudengang erfolgt üblicherweise in doppel logarithmischer Achsenskalierung (auch halblog ist manchmal sinnvoll). Der Phasengang normalerweise in Winkelgraden.
Zur Berechnung des Amplitudengang ist aus der komplexen Zahl, die die Übertragungsfunktion ja ist, der Betrag dieser komplexen Zahl zu bilden
Zur Berechnung des Phasengangs ist der arcus tangens der komplexen Übertragungsfunktion.
In der Praxis überläßt man diese Aufgabe für komplizierte Netzwerke am besten einem symbolischen Rechenknechten, der das mit einer Zeile Code erledigt. Das Diagramm kann dann problemlos geplottet werden.
Da aber die komfortable Darstellung die einzelnen Glieder mulitplikativ verbindet entspricht dies in logarithmischer Darstellung einer Addition der Pol- und Nullstellen und diese ist sehr einfach grafisch mit einem Stück Papier darstellbar. Selbst wenn für einzelne Frequenzen diskrete Amplituden- und Phasenwerte berechnet werden müssen, dazu genügt ein einfascher Taschenrechner mit komplexer Eingabemöglichkeit. Die Berechnung der Gleichungen für Amplituden- und Phasengang ist nur komplexe Mathematik, im Prinzip ist es Geometrie, darauf möchte ich hier jetzt nicht eingehen und werde dies vielleicht einmal in einem gesonderten Bericht behandeln.
Zweites Beispiel
um zu beweisen, daß die bisher gezeigten Methoden auch für andere Schaltungen gelten, füge ich gern noch ein anderes Beispiel hinzu. Es wird genau die empfohlene Reihenfolge eingehalten.

Bild 16
Schritt 1: Schaltung unterscheiden in invertierenden oder nicht invertierenden Verstärker, die jeweilige ideale Grund-Übertragungsfunktion ist anzuwenden, 1+(X1/X2) für nichtinvertierende und -X1/X2 für invertierende Schaltungen; (gelingt nicht bei allen Schaltungen). Hier ist es eine nicht invertierende Schaltung.

Bild 17
Schritt 2: Esatzschaltbild für X1 bilden, dabei Kondensatoren als Xc und Induktivitäten als XL behandeln
Schritt 3: Esatzschaltbild für X2 bilden, dabei Kondensatoren als Xc und Induktivitäten als XL behandeln
Schritt4: X1 und X2 in die jeweilige Grundgleichung des invertierenden oder nicht invertierenden Verstärker einsetzen.

Bild 18
Schritt 5: den Übergang in die komplexe Zahlenebene durchführen, in dem Xc durch 1/jwC und XL durch jwL ersetzt werden.

Bild 19
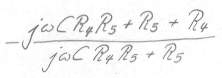
Bild 20
Schritt 6: Reduzierung der vielen Brüche auf einen einzigen verbleibenden, mit nur einem Zähler und nur einem Nenner, jede mathematische Methode hierzu sei willkommen.
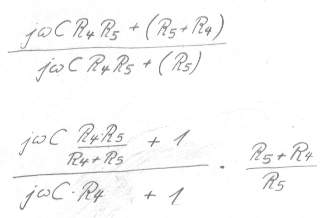
Bild 21
Schritt 7: im Zähler wird
genau der Term ausmultipliziert, der dazu führt daß alle "ScheinbarTau"
Zeitkonstanten des Zählers die Einheit Sekunde bekommen. Zudem muss bei Pol-
und Nulllstellen zwingend die "+1" entstehen. Wenn sie nicht entsteht ist
es ein Differenzierendes Glied.
Schritt 8: im Nenner wird genau der Term ausmultipliziert, der dazu führt daß alle "ScheinbarTau" Zeitkonstanten des Nenners die Einheit Sekunde bekommen. Zudem muss bei Pol- und Nullstellen zwingend die "+1" entstehen. Wenn sie nicht entsteht ist es ein Integrator.
Schritt 9: Vereinfachen und Ausmultiplizieren von jwC, in diesem Fall war dies gar nicht notwendig.
Schritt 8: im Nenner wird genau der Term ausmultipliziert, der dazu führt daß alle "ScheinbarTau" Zeitkonstanten des Nenners die Einheit Sekunde bekommen. Zudem muss bei Pol- und Nullstellen zwingend die "+1" entstehen. Wenn sie nicht entsteht ist es ein Integrator.
Schritt 9: Vereinfachen und Ausmultiplizieren von jwC, in diesem Fall war dies gar nicht notwendig.
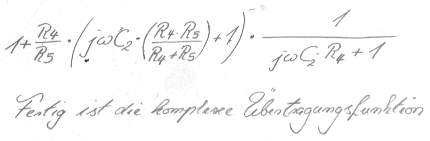
Bild 22
Schritt 10: Gleichung noch etwas aufräumen und Pol- und Nullstellen einzeln hintereinander hinschreiben.
Ist doch ganz einfach oder?
Ein graphisches Beispiel für den Frequenzgang der gezeigten Funktion

Tutorial Impressum