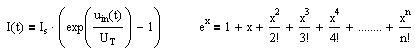Nonlinear Distortions

Nonlinear distortions result in an amplifier from nonlinear curve characteristics of the parts.

Linear distortions do not produce new frequencies. If the original signal no new frequencies are in addition-mixed, linear distortions develop.

Introduction

Nonlinear distortions have clear effects on the sound. They are a dominant factor source for disturbances. It is one of the highest targets with the development of a Hifi amplifier of keeping the nonlinear distortions small.

Strictly linear conditions do not exist in electro-technology. Everything, whatever is called as linear, is nonlinear in reality. The question is only, which order of magnitude has the non-linearity? Much can be called confidently simplified linear. Transistors and tubes are particularly nonlinear. Depending upon operating point, the characteristics have a usually exponential character. In some characteristic sections also an overlaid square characteristic is present. Very linear elements are resistances. Some condensers are also still linear.

Unfortunately the active amplifiying elements are nonlinear. The characteristics of transistors, diodes and tubes are clearly temperature and voltage-dependently. If the gain of these active elements would be linear, the building of an amplifier would be clearly simpler. The number of elements would reduce drastically. But nature is merciless in this regard and gives no consideration to the desires of a developer.

Nonlinear distortions make visible

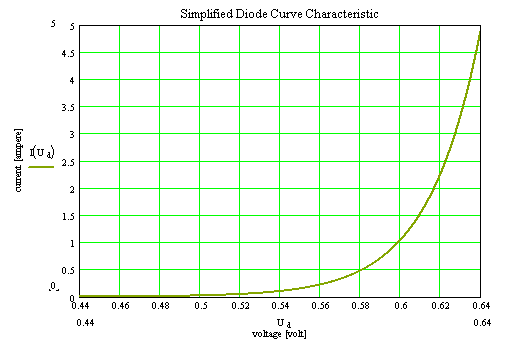
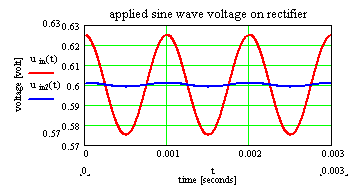
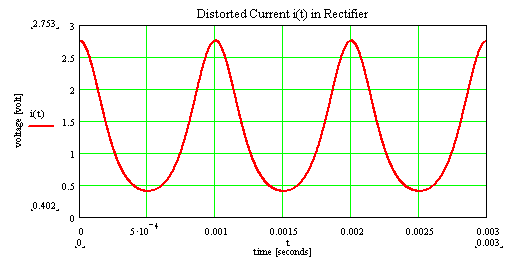
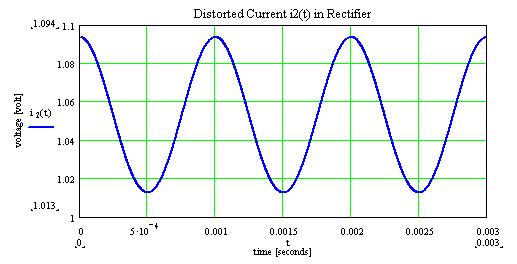
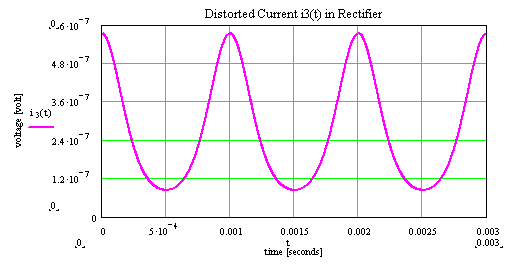
As an aid here a model for a simple diode serves. The nonlinear distortions caused by the diode, are made on the basis the curve characteristics visible. The diode characteristics is based in a simple model of a diode. At the diode a sinus-wave voltage with offset is applied. The resulting current by the diode is not linear any longer. It contains new frequencies.

parameter of simulation
Figure 1 shows the characteristic of a diode, based on a simple exponential function.

 

Figure 2 shows the test voltages. A sine wave voltage with a frequency of 1 kHz, an amplitude of 25 mV and 1 mV is used. As offset 600 mV are adjusted.
The two test sine wave voltages used in the diode equation.

Figure 3 shows the current i(t) by the diode. Since the characteristic of the diode is nonlinear, now also the current became nonlinear by the diode. To see clear, the current is no longer sinusoidally separates distorted. With a linear resistance now also the current would be sinusoidal.

Figure 4 shows the current i2(t) by the diode. Here now the amplitude of the alternating voltage was reduced. Remarkably in this representation, which seems current now only minimum distorted. That is only an optical deception, distortions is also present. The amplitudes of the distortions became smaller around a multiple.

As model for the diode curve characteristics an exponential function was used. The mathematical derivative of an exponential function is again an exponential function. For this model meant that here, all the same in which place in the characteristic by the offset the sinusoidal voltage is put on, the distortions remain the same. To material considerations this consideration applies only reduced, since the characteristic of the diode has an exponential character, but not exclusive.

Here now a sine wave voltage put on with a changed offset of only 200 mV. The amplitude is 25 mV as in fig. 3

Bild 5 shows the same process as only in fig. 3, with lower amplitudes.

Continue to divide into spectral components leaves itself an exponential function by means of a Taylor of polynomial. I do without the execution.

With the Taylor polynomial or a Fourier analyses can the current into its frequencies further be divided.

Measure of nonlinear distortions

Expressions for nonlinear distortions exist several, however no clear unit. The result of measurement can be a spectrum, or only a simple number e.g. the distortion factor.

  • Nonlinear distortions can be measure with analogue spectrumanalyzers e.g. HP 3580A, 7L12 or with a selective voltmeter e.g. HP 3581A, HP 3586C. The selection of further measuring instruments at the market is large. Their effect principle is similar mixture with tunable filter.

  • A further group works according to the principle of digital signal processing. A AD converter digitizes the signal and a computer accomplishes a Fourier transformation. In addition special measuring instruments in addition, e.g. sound cards belong in a computer, if these are consulted for the measurement. They deliver e.g. a spectrum and the distortion factor at the same time.

  • A further group are distortion factor of measuring instruments e.g. HP 8903A/B, HP 333, HP 334 or HP 339, as well as many other manufacturers. There is tunable filters, those as result directly a number, the distortion factor indicates.

  • to determine nonlinear distortions leave themselves to precise voltmeter also with the help of by measuring the curve characteristic, e.g.. with a HP 3457A or HP 34401A. The won curve characteristics can be analyzed with analytic mathematics.

The methods are various and everyone have their special advantages and disadvantages.

Tutorial Index     www.amplifier.cd      Contact