Geradzahlige Harmonische in Rechteckspannungen


Ein Leser interessierte sich dafür wie hoch die geradzahligen Frequenzanteile in Rechteckspannungen sind und bat um einen Vergleich aus verschiedenen Quellen. 

"Ich benötige einen Rechteckgenerator (er soll 3,2 KHz erzeugen) , dessen gerade 
Harmonische sich unter dem Noisefloor eines 3580 verstecken können...Also -90 dB.

Nach bisherigen Betrachtungen sollte er schnell sein (steile Flanken), und sein 
Tastverhältnis sollte exakt 50% und Jitterfrei sein.

Das ist alles leicht gesagt, denn meine drei (teuren)Pulsgeneratoren, sowie alle hier 
stehenden Rechteckgeneratoren kommen dieser Forderung nicht! ausreichend nach.

tiefer als -80 dB geht es hier nicht."

Gerät 1: 1kHz Kalibratorausgang aus dem Oszilloskop.

von diesem Ausgang wird eine exakte Amplitude erwartet, um die Kette Tastkopf und Vertikalverstärker exakt auf 2 Division im Vertikalraster einzustellen. Ebenso soll die ansteigende und fallende Flanke gerade sein, damit auch der kapazitive Spannungsteiler z.B. eines 1:10 Tastkopfes exakt eingestellt werden kann.

Messaufbau aus 7704A und 3580A.

Der Kalibrator hat ca. 1kHz und 400mV Amplitude. Das Pulsweitenverhältnis habe ich nicht gemessen. Der analoge Generator ist recht jitterarm.

 
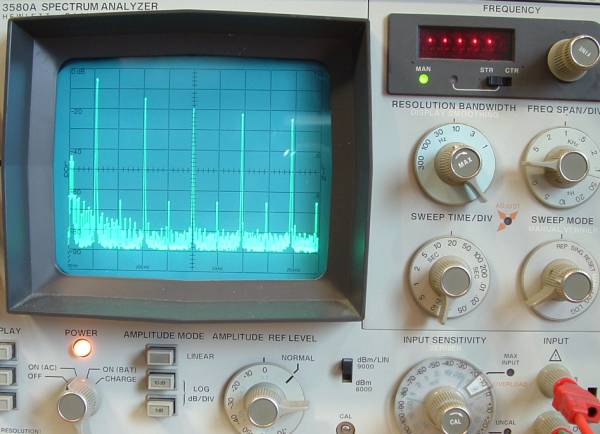 das 1 kHz Kalibrator Signal folgt der Fourier Theorie, zeigt aber auch geradzahlige Anteile etwa 60 dB unterhalb der Grundwelle. Analyzer Einstellung hier: 1kHz/DIV, Startfrequenz DC. Das Pulseitenverhältnis liegt mit dem Oszillogramm bewertet nahe an 50:50.


Gerät 2: steilflankiger Rechteckgenerator mit 4kHz

dieser Rechteckgenerator zeichnet sich aus durch eine wahlweise sehr steile fallende oder ansteigende Flanke. Die Steig- oder Fallzeiten liegen unterhalb einer Nanosekunde. Damit läßt sich beispielsweise die Slew Rate sehr schneller Verstärker ausmessen.  Oder austesten wie ein elektrisches System auf eine "nahe" ideale schnelle Sprungantwort reagiert. Die Einhaltung eines idealen PWM Verhältnisses ist bei diesen Generatoren normalerweise kein Desingkriterium.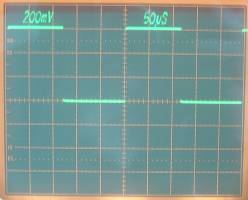

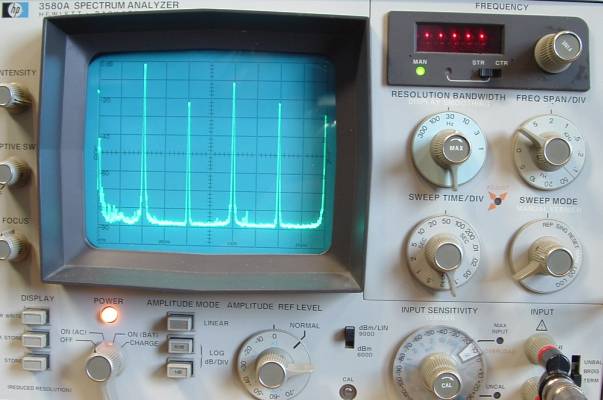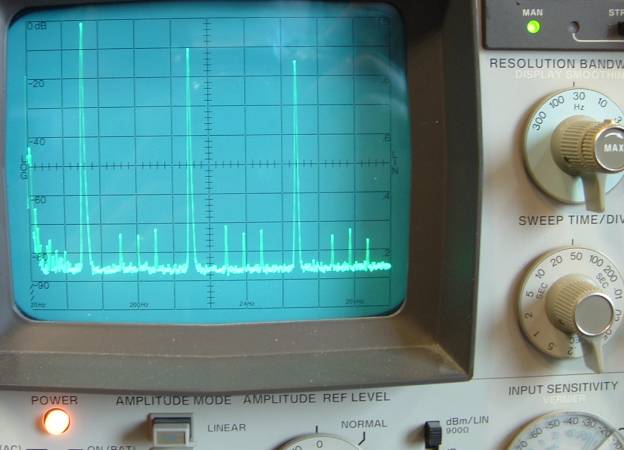
Der Analyzer steht auf 2kHz/DIV. Das 4kHz Rechteckt zeigt hohe Anteile an geradzahligen Oberwellen, trotz schneller fallender Flanke. Die ansteigende Flanke ist langsamer und stört die Symmetrie, auch das Pulsweitenverhältnis beträgt nicht exakt 50:50, siehe Oszillogramm. Die Symmetrie ist zwar einstellbar, ich habe bei der Messung allerdings nicht darauf geachtet. Auch diese Rechteckspannung ist recht jitterarm.

Der Generator wurde mit 50 Ohm abgeschlossen.


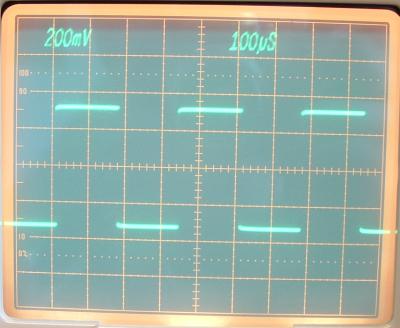
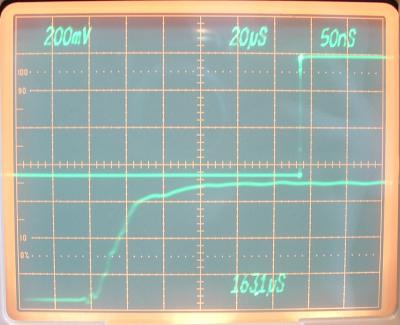
 Gerät 3: Syntheziser Frequenzgenerator

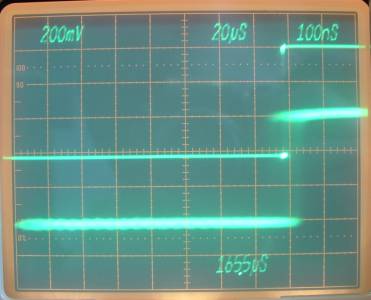
Verwendet wurde hier ein digitaler Generator, der sich dadurch auszeichnet, dass seine Ausgangsfrequenzen äußerst präzise und sehr hoch auflösbar sind. Das Gerät besitzt sogar einen Ofenquarz.

Prinzipbedingt hat dieser Generator einen höheren Jitter als manche analogen Geräte. Das Oszillogramm zeigt dieses Verhalten deutlich.

Im Oszillogramm wurde die ansteigende Flanke um den Faktor zweihundert gezoomt dargestellt. Die ansteigende Flanke des gezoomten Graphen steht nicht still bezogen auf das Triggersignal der ungedehnten Darstellung.

Der Generator hält aber dagegen wahrscheinlich das Pulsweitenverhältnis 50:50  ein.

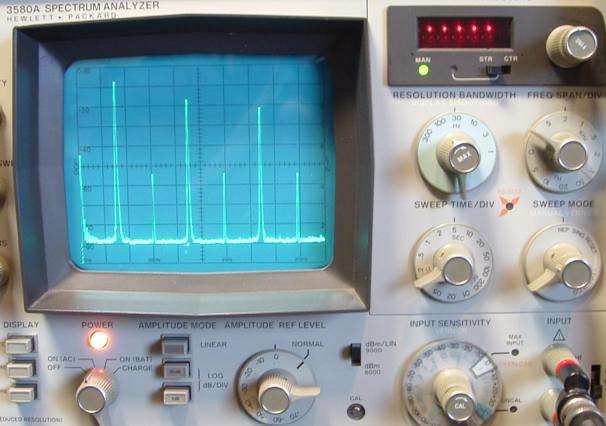
Der Analyzer steht hier auf 2kHz/DIV. In der Resolution Bandwidth wurde noch eine Stufe des Video "smoothing" Filter zugeschaltet (das kleine Drehrädchen max. im Resolution Knopf), dadurch werden in der Analyzer Base Line nochmals kleine nichtperiodische Peaks ausgefiltert, allerdings steigt dadurch die notwendige Sweep Time auf mindestens 50s/DIV an.

Das 3kHz Rechtecksignal zeigt nur einen geringen Anteil an geradzahligen Frequenzanteilen. Sehr stark auffällig sind jedoch die neu entstandenden Mischprodukte jeweils rechts und links von den geradzahligen Frequenzanteilen. Diese Beobachtung trat bei den analogen Generatoren nicht auf.

Diese zusätzlichen unerwünschten Mischprodukte sind sehr wahrscheinlich ein Ergebnis des höheren Generator Jitters, der seine Ursache im Funktionsprinzip hat.


Gerät 4: Low Distortion Sine Generator im Rechteckmodus



Hier wird ein sehr klirrarmer Sinusgenerator verwendet, der auch eine Taste für einen Rechteckbetrieb hat. Man sieht schon aus der Ferne, der kann es auch nicht.

       

Dieser analoge Generator hat am Oszilloskop zumindest 50:50 der Anstieg ist mit über 100ns nicht besonders schnell, allerdings steht die Frequenz ohne am Oszilloskop erkennbaren Jitter, die Darstellung wurde hier immerhin um den Faktor 400 gezoomt und steht ausgezeichnet still, man vergleiche mal Gerät 3 hierzu.


Gerät 5: ein Multifunktionsgenerator

Hier wurde nun ein Multifunktionsgenerator verwendet, auch er schafft es nicht eine Konstantheit der Pulsweite 50:50.

Zwei Generatoren hab ich noch, die hier noch später getestet werden, alles Pulver ist also noch nicht verschossen. Es steht auch noch der Versuch aus, den schnellen 106 einmal in der Pulsweite soweit zu verstellen, bis die geradzahligen Frequenzanteile minimal werden. Auch werde ich mal den Kalibrator im Digitaloszi testen und hier anfügen oder mir mal mit Gattern, OP's mal was selber bauen - alles irgendwann mal, nur nicht morgen.

Anonsten interessant ist das Ergebnis mit dem Synthesizer, der Jitter verursacht anscheinend Mischprodukte um die geradzahligen Frequenzanteile herum, das wurde nur bei diesem Funktionsprinzip beobachtet. Ich denke der Schlüssel liegt in einer einigermaßen schnellen gleichen Anstiegs- und Abfallzeit, einem sehr genauen 50:50 Pulsweitenverhältnis und einer Konstantheit der Kurzzeitstabilität der Frequenz, also im Prinzip niedriger Jitter. Wer sowas braucht, hat sicherlich zuerst einmal ein Problem bis er was geeignetes findet, ich brauche es zum Glück im Moment nicht.

Andreas hat zu seiner Fragestellung die Ergebnisse seiner Generatoren freundlicherweise zur Verfügung gestellt:

Allen folgenden Text hat Andreas verfasst:

Auslöser für die Suche nach einem Rechteckgenerator "ohne" geradzahlige Oberwellen war die Messung transienter Intermodulation (TIM) an Audioverstärkern. Zwar war ich schon seit geraumer Zeit im Besitz eines RE-201 Audioanalyzers, welcher auch die entsprechenden Signale liefert, aber seine "Messtiefe" wurde laut Spezifikationen mit lediglich mit 0,02% angegeben. Unerwünschte, geradzahlige Harmonische sind  noch deutlich zu erkennen.

Das benutzte "TIM-100" Meßsignal besteht aus einem 3,18 KHz Rechteck, dem nach passieren eines  100KHz Filter erster Ordnung, ein 15 KHz Sinus zugemischt wird. Dabei beträgt das Amplitudenverhältnis vier zu eins. Dieses Meßverfahren wurde schon vor über 20 Jahren angewendet.

Ich habe daraufhin  ettliche Rechteckgeneratoren überprüft und musste feststellen, dass es nicht so einfach ist, einen Generator zu finden, der den Anforderungen  entspricht. Bei dieser Gelegenheit kam auch mein "neuer" Chartplotter PM8143 zum Einsatz, der von einem HP3580A angesteuert wurde. Den sehr gut erhaltenen  "Oldtimer" konnte ich vor Kurzem incl. etlicher Stifte günstig erwerben. Die X-Achse am Plotter ist (noch) nicht immer absolut korrekt ausgerichtet...Ich arbeite noch daran. Es ist eine ziemliche Fummelei.


Gerät 6: Audio Analysator

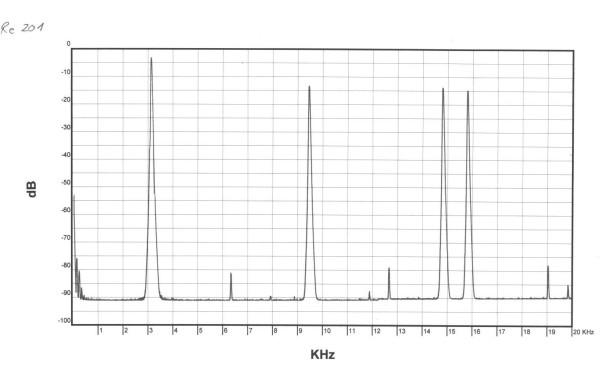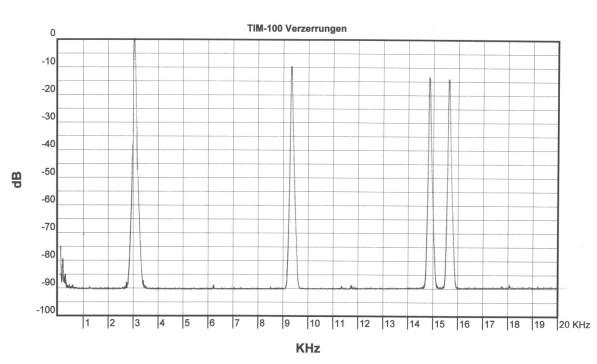
Der RE201 ist ein seltenes Spezialgerät zur Audioanalyse. Der Plot zeigt das Ergebnis der TIM Analyse mit dem Re201.


Gerät 7: LF Synthesizer

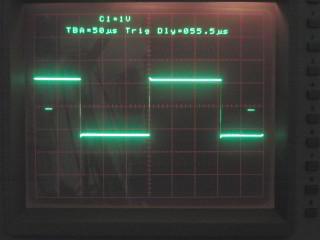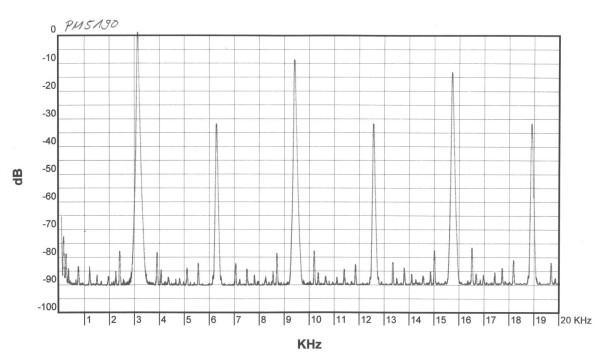Der PM5190  machte in meinem Vergleich die "schlechteste Figur". Er erzeugte einen vergleichsweise starken Jitter  und war mit rund 50 ns Anstiegszeit auch nicht besonders steil. Zahlreiche Mischprodukte und ausgeprägte geradzahlige Harmonische prägen das Bild. Die Amplituden des Rechtecksignals sind zudem um etwa 200 mV verschieden. Zwar konnte das durch die Offseteinstellung  am Gerät auskompensiert werden, aber das Gerät muss ich dringenst mal "nachkalibrieren". Zwar sind Amplitude und Frequenz des digitalen Generators sehr stabil, aber für meinen Zweck ist das Rechtecksignal dieses Generators ungeeignet.


Gerät 8: analoger Pulsgenerator

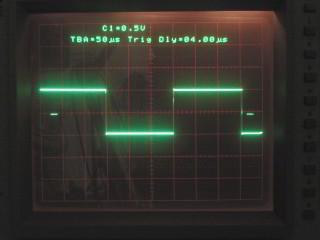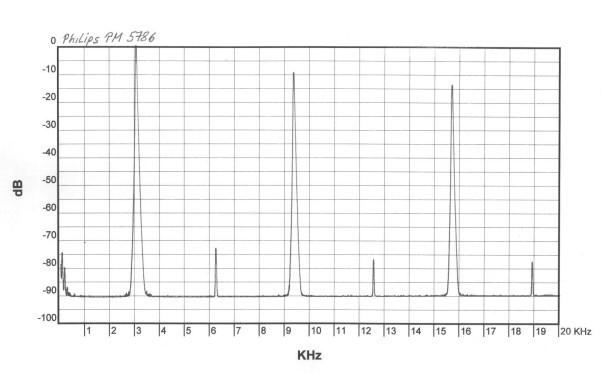Der PM5786 Pulsgenerator war zu Anfang einer meiner Favoriten. Trotz einer minimal einstellbaren Anstiegs- und Abfallzeit von nur 2 ns und einer auf dem Oszilloskop einwandfreien, visuell symmetrischen Rechteckwiedergabe, waren geradzahlige Oberwellen vorhanden. Der Pegel dieser Oberwellen stieg bis zu einer Anstiegszeit von etwa 20 ns auch nicht nennenswert weiter an. Hier dürfte die Symmetrie des Signals der limitierende Faktor sein. Das Gerät kann wahlweise auch auf 50% Tastverhältnis "fest" eingestellt werden. Eine variable Einstellung des Tastverhältnisses über Potentiometer machte sehr schnell deutlich, um welche Toleranzen es hier geht. Es war mir manuell nicht möglich, auch nur annähernd das Spektrum des  50/50 Festwertes zu erreichen.


Gerät 9: Function Generator

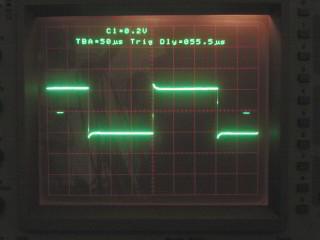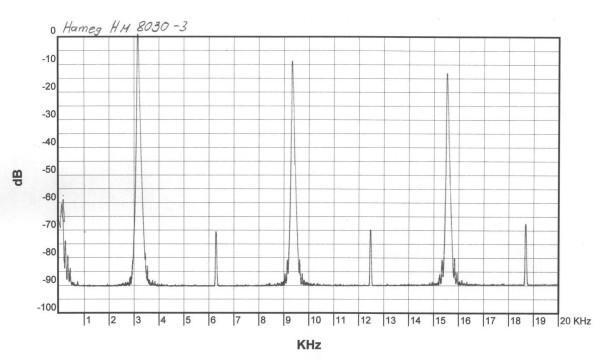Der Hameg 8030 zeigte trotz 50 Ohm Abschluss einen ausgeprägten "overshoot". Dabei ist die Anstiegsazeit mit  30 ns noch nicht einmal besonders kurz. Auffällig sind die vergleichsweise  ausgeprägten Seitenbänder an  der Grundwelle und ihren ungeraden Harmonischen. Ich habe in Erinnerung, dass der Generator nicht immer dieses schlechte Ergebnis (Überschwinger) lieferte und vermute einen Defekt im Bereich der Frequenzkompensation des Ausgangsverstärkers.


Gerät 10: Arbiträrer Function Generator

Zum Schluss habe ich ziemlich ernüchtert noch einen älteren, arbiträren Funktionsgenerator von LeCroy ausprobiert. Er hat die Standardsignale Triangle, Sine und Square (50/50) bereits in seinem Rom integriert. Tastverhältnis, Frequenz und Amplitude können über eine Kabelfernbedienung mit LC-Display, oder über die GPIB Schnittstelle verändert werden. Dazu kann man z.B. die LeCroy Software "Easywave" oder auch "Labview" benutzen. Ebenso kann man mit diesem Generator nahezu jede beliebige Signalfolge Generieren oder Aufzeichnen und in weitreichender Frequenz ausgeben. Die Anstiegs und Abfallzeit des Rechtecks beträgt rund  5 nS. Rein "visuell" gibt es am Signal keinerlei Auffälligkeiten. Verblüffend ist jedoch das eigentliche Ergebnis der Spektralanalyse. Keine geradzahligen Harmonische und keinerlei Mischprodukte erkennbar.

Perfekt für meinen Zweck.

Im Spektogramm ist das kombinierte TIM-100 Signal des  Generators zu erkennen.

Der 15 KHz Sinus stammt von einem klirrarmen Generator und ist weitgehend unkritisch. Filterung und Mischung habe ich rein passiv realisiert.


Andreas ich danke Dir sehr für die interessante Fragestellung, deine Messungen, die Fotos, den Text und die ganze Arbeit. Es wurde klar welche Parameter von Interesse sind und auch welches Funktionsprinzip der Generatoren für die Anwendung geeignet ist.
Auch den Chartplotter finde ich klasse, die X-Y Ausgänge am Spektrumanalyzer sind präziser als das Ergebnis in der CRT, die Schreiberausgänge liefern das echte Meßsginal, eine CRT fügt durch ihren Verzug, Kissen, Astigmation (je nach Kalibrationszustand) meistens einen geringen Fehler hinzu. Wie hast Du den die Zahlen und Linien gedruckt, zuvor mit dem PC-Drucker entsprechend auf dem Papier skaliert?


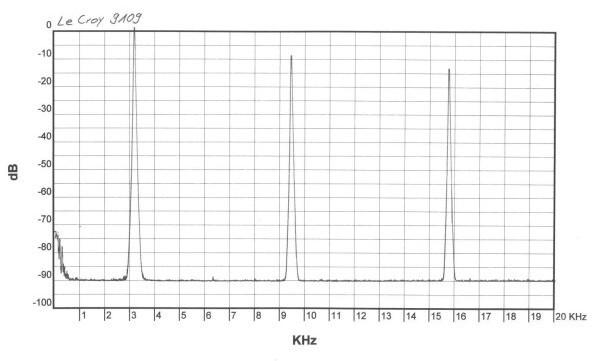Ein Leser, der liebe "klausthal" hat mir eine Email zugesandt, die ich gern veröffentliche.
Dankeschön "klausthal" für diese Korrektur.

Hallo, Ralf,

ich habe Deinen Bericht "Geradzahlige Harmonische in Rechteckspannungen" mit Interesse gelesen. Die mathematische Fourieranalyse zeigt unmittelbar, dass wegen langsamen Flankenanstiegs des Rechtecksignals KEINE geraden Harmonischen entstehen! Das folgt schon aus der Tatsache, dass die Fourierentwicklung einer GERADEN Funktion f(t) nur geradzahlige Harmonische, die einer UNGERADEN Funktion nur ungeradzahlige Harmonische aufweist. (Erinnerung: f(t) heisst gerade, wenn f(t)=f(-t), und sie heisst UNgerade, wenn f(t)=-f(-t)). Eine Rechteckschwingung mit schrägen Flanken kann durch eine Trapezschwingung approximiert werden und ist ungerade.
 
Demzufolge nützt die Suche nach einem Generator mit möglichst steilem Flankenanstieg rein nichts, und die Ursache für das Auftreten der unerwünschten geradzahligen Harmonischen muss woanders gesucht werden.
 
Ich hoffe, ich konnte helfen.
 
klausthal




home

Fragen     Impressum und Haftungsausschluß